题目内容
20.己知(ax-3)(-x+b)=mx2+11x-12,则a=2,b=4,m=-2.分析 根据(ax-3)(-x+b)=mx2+11x-12,把原始左边展开,然后根等号左右两边对应项的系数相等,可以得到a、b、m的值,本题得以解决.
解答 解:∵(ax-3)(-x+b)=mx2+11x-12,
∴-ax2+(ab+3)x-3b=mx2+11x-12,
∴$\left\{\begin{array}{l}{-a=m}\\{ab+3=11}\\{-3b=-12}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=2}\\{b=4}\\{m=-2}\end{array}\right.$
故答案为:2,4,-2.
点评 本题考查多项式乘以多项式,解题的关键是找准对应关系,求出所求问题的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知直角三角形两边的长分别为5、12,则第三边的长为( )
| A. | 13 | B. | 60 | C. | 17 | D. | 13或$\sqrt{119}$ |
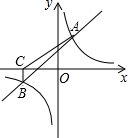 如图,一次函数y1=x+1与反比例函数y2=$\frac{k}{x}$的图象相交于点A(2,3)和点B.
如图,一次函数y1=x+1与反比例函数y2=$\frac{k}{x}$的图象相交于点A(2,3)和点B.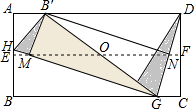 数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.
数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.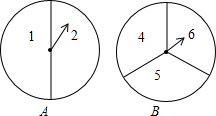 如图,有两个可以自由转动的均匀转盘A、B,分别被分成2等份和3等份,每份内均都有数字.小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.
如图,有两个可以自由转动的均匀转盘A、B,分别被分成2等份和3等份,每份内均都有数字.小明和小亮用这两个转盘做游戏,游戏规则如下:分别转动转盘A和B,两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止),若和为偶数,则小明获胜;如果和为奇数,那么小亮获胜.