题目内容
8.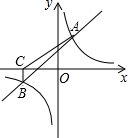 如图,一次函数y1=x+1与反比例函数y2=$\frac{k}{x}$的图象相交于点A(2,3)和点B.
如图,一次函数y1=x+1与反比例函数y2=$\frac{k}{x}$的图象相交于点A(2,3)和点B.(1)求反比例函数的解析式y2=$\frac{6}{x}$.
(2)过点B作BC⊥x轴于C,求S△ABC.
(3)若点P(x1,y1)、Q(x2,y2)在函数的图象上,且x1<x2,试比较y1与y2的大小.
分析 (1)利用待定系数法求出反比例函数的解析式;
(2)列出方程组,求出点B的坐标,根据三角形的面积公式计算即可;
(3)根据反比例函数的性质、运用数形结合思想和分情况讨论思想解答即可.
解答 解:(1)∵反比例函数y2=$\frac{k}{x}$的图象经过点A(2,3),
∴3=$\frac{k}{2}$,
解得k=6,
∴反比例函数的解析式为y2=$\frac{6}{x}$,
故答案为:y2=$\frac{6}{x}$;
(2)$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{6}{x}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-2}\end{array}\right.$,
∴点B的坐标为(-3,-2),
∴BC=2,
∴S△ABC=$\frac{1}{2}$×2×(3+2)=5;
(3)当0<x1<x2时,y1>y2;
当x1<x2<0时,y1>y2;
当x1<0<x2时,y1<y2.
点评 本题考查的是反比例函数与一次函数的交点问题以及反比例函数的图象和性质,灵活运用待定系数法求函数解析式、掌握反比例函数的性质是解题的关键.

练习册系列答案
相关题目
19.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,则代数式x02-(x1+x2)x0+x1x2的值( )
| A. | 等于0 | B. | 恒正 | C. | 恒负 | D. | 不能确定 |
13.政府去年对某校的投资为2百万元,预计今明两年的投资总额为8百万元,设政府对该校这两年投资的平均增长率为x,则可列方程为( )
| A. | 2(1+x)2=4 | B. | 2(1+x)2=8 | C. | 2(x+2)2=8 | D. | 2(x+1)(x+2)=8 |
17.在下列各选项中给出的三条线段不一定能组成三角形的是( )
| A. | a+1,a+2,a+3(a>0) | B. | 三条线段的比是4:6:8 | ||
| C. | 3cm,8cm,10cm | D. | 3a,5a,2a+1(a>0) |
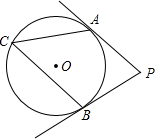 如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.
如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.