题目内容
2.关于x的方程(m-3)x|m|-2+8=0是一元一次方程,则该方程的解是x=$\frac{8}{3}$.分析 根据题意得出m的等式,进而解方程即可.
解答 解:∵关于x的方程(m-3)x|m|-2+8=0是一元一次方程,
∴|m|-2=1,
解得:m=±3,
∵m-3≠0,
∴m≠3,
∴m=-3,
则方程为:-3x+8=0,
解得:x=$\frac{8}{3}$.
故答案为:x=$\frac{8}{3}$.
点评 此题主要考查了解一元一次方程,正确得出m的值是解题关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.一个多项式A减去多项式2x2+5x-3,某同学将减号抄成了加号,运算结果为-x2+3x-5,那么正确的运算结果是( )
| A. | -3x2-2x-4 | B. | -x2+3x-7 | C. | -5x2-7x+1 | D. | 无法确定 |
17.下列图形中是棱锥的侧面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
7.抛物线y=x2-2x+3 的对称轴为( )
| A. | 直线x=-1 | B. | 直线x=-2 | C. | 直线x=1 | D. | 直线x=2 |
14.下列计算中正确的是( )
| A. | -23•(-2)0=0 | B. | (-2x2y3)3=6x6y9 | ||
| C. | (3m+n)•(-n+3m)=9m2-n2 | D. | (-a)3÷(-a)=-a2 |
12.已知:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,在下列条件中,不能判定$\overrightarrow{a}$∥$\overrightarrow{b}$的是( )
| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=3$\overrightarrow{c}$,$\overrightarrow{b}$=-$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | $|{\overrightarrow a}|=2|{\overrightarrow b}|$ |
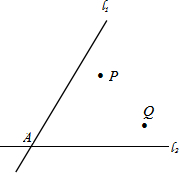 尺规作图:如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(保留作图痕迹)
尺规作图:如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(保留作图痕迹)