��Ŀ����
��֪һԪ���η���ax2+bx+c=0��a��0���У�����˵����
����a+b+c=0����b2��4ac��0��
��������������1��2����2a+c=0��
��������ax2+c=0����������ȵ�ʵ������ax2+bx+c=0������������ȵ�ʵ����
����b=2a+c��������������ȵ�ʵ����������ȷ���У�������
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
C ������������������ٵ�ʱ������ ��������ʵ�����ˣ� �ʴ��� �ڰ� ���뷽�̵õ�����1�� �Ѵ��뷽�̵õ��� ��2�� �ѣ�2��ʽ��ȥ��1��ʽ��2�õ��� ���� ����ȷ�� �۷��� ����������ȵ�ʵ������ ������ �����̵� �������������ȵ�ʵ����������ȷ�� ������ ����ȷ�� �ڢۢܶ���ȷ�� ��ѡC��
��ϰ��ϵ�д�
�����Ŀ




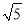 B.
B. 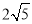 C.
C. 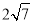 D.
D. 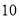
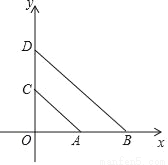
 �ڵ�һ����ͼ��С���������¶���E����OB2��BE2=10����k��ֵ�ǣ�������
�ڵ�һ����ͼ��С���������¶���E����OB2��BE2=10����k��ֵ�ǣ�������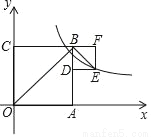
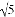
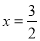 ��������ò�ͬ�ĺ�������ʽ��ʾ��������ѡ����һ����д������ʽ��
��������ò�ͬ�ĺ�������ʽ��ʾ��������ѡ����һ����д������ʽ��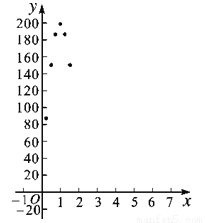
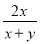 �е���ĸ
�е���ĸ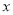 ��
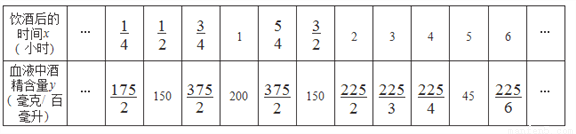
��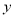 ��ֵ�ֱ�����Ϊԭ����10�����������ʽ��ֵ�� ��
��ֵ�ֱ�����Ϊԭ����10�����������ʽ��ֵ�� ��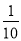 ��
��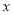 �ķ���
�ķ���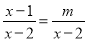 ����������
����������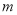 ��ֵ��___________.
��ֵ��___________.