题目内容
三角形的一个内角为30°,有两边分别为3,4.这样的三角形有几个?请说明理由.
考点:三角形边角关系
专题:分类讨论
分析:由于符合要求的三角形不唯一,需分情况讨论.可按30°角的对边的长度进行分类:①若30°角的对边的长度既不是3又不是4,②若30°角的对边的长度是3,③若30°角的对边的长度是4.结合画图就可解决问题.
解答:解:符合条件的三角形共有四个.
理由如下:
①若30°角的对边的长度既不是3又不是4,
作∠MAN=30°,在AM上取一点B使得AB=4,在AN上取一点C使得AC=3,连接BC,如图1.

由SAS可得这样的三角形只有一个.
②若30°角的对边的长度是3,
作∠MAN=30°,在AM上取一点B使得AB=4,过点B作BH⊥AN于H,
∵∠A=30°,AB=4,∠AHB=90°,
∴BH=
AB=2<3,BA>3.
∴以点B为圆心,3为半径画弧,必与射线AN有两个交点,设交点为C,连接BC,如图2和图3.


可见这样的三角形有两个.
③若30°角的对边的长度是4,
作∠MAN=30°,在AN上取一点C使得AC=3,
∵CA<4,
∴以点C为圆心,4为半径画弧,与射线AM只有一个交点B,连接BC,如图4.

可见这样的三角形只有一个.
综上所述:符合条件的三角形共有四个.
理由如下:
①若30°角的对边的长度既不是3又不是4,
作∠MAN=30°,在AM上取一点B使得AB=4,在AN上取一点C使得AC=3,连接BC,如图1.

由SAS可得这样的三角形只有一个.
②若30°角的对边的长度是3,
作∠MAN=30°,在AM上取一点B使得AB=4,过点B作BH⊥AN于H,
∵∠A=30°,AB=4,∠AHB=90°,
∴BH=
| 1 |
| 2 |
∴以点B为圆心,3为半径画弧,必与射线AN有两个交点,设交点为C,连接BC,如图2和图3.


可见这样的三角形有两个.
③若30°角的对边的长度是4,
作∠MAN=30°,在AN上取一点C使得AC=3,
∵CA<4,
∴以点C为圆心,4为半径画弧,与射线AM只有一个交点B,连接BC,如图4.

可见这样的三角形只有一个.
综上所述:符合条件的三角形共有四个.
点评:本题考查了三角形的边角关系、30°角所对的直角边等于斜边的一半、直线与圆的位置关系、全等三角形的判定(SAS)等知识,考查了动手操作的能力,还考查了分类讨论的思想,而选择一个适当的分类标准是解决本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 8个一样大小的长方形恰好拼成一个大的长方形(如图1),也可以拼如图2那样的正方形,但这个大正方形中间恰好留下了一个边长为2cm的小正方形.则每一个小长方形的面积为( )
8个一样大小的长方形恰好拼成一个大的长方形(如图1),也可以拼如图2那样的正方形,但这个大正方形中间恰好留下了一个边长为2cm的小正方形.则每一个小长方形的面积为( )| A、32cm2 |
| B、56cm2 |
| C、60cm2 |
| D、64cm2 |
 如图,△ABC中,已知,DE∥BC,AE:EC=3:2,求AB:DB,AB:AD的值.
如图,△ABC中,已知,DE∥BC,AE:EC=3:2,求AB:DB,AB:AD的值.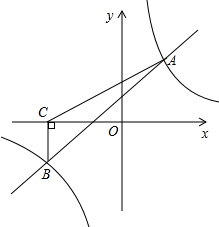 如图,一次函数y=kx+b与反比例函数y=
如图,一次函数y=kx+b与反比例函数y= 如图,在矩形ABCD中,已知AD=10,AB=8,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,求CE的长.
如图,在矩形ABCD中,已知AD=10,AB=8,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,求CE的长. 如图,已知
如图,已知 指出下列几何体的截面形状.
指出下列几何体的截面形状. 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论: