题目内容
1.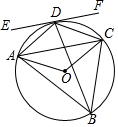 如图,⊙O是△ABC的外接圆,连接OA,OC,BD平分∠ABC,交⊙O于点D,连接AD,CD,过点D作直线EF∥AC,已知∠BDC+∠ACB=130°.
如图,⊙O是△ABC的外接圆,连接OA,OC,BD平分∠ABC,交⊙O于点D,连接AD,CD,过点D作直线EF∥AC,已知∠BDC+∠ACB=130°.(1)求∠ABC的度数;
(2)求证:直线EF是⊙O的切线.
分析 (1)由圆周角定理,可得∠BDC=∠BAC,又由∠BDC+∠ACB=130°,即可求得答案;
(2)首先连接OD,由BD平分∠ABC,易证得OD⊥AC,又由直线EF∥AC,证得结论.
解答 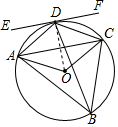 (1)解:∵∠BDC=∠BAC,∠BDC+∠ACB=130°,
(1)解:∵∠BDC=∠BAC,∠BDC+∠ACB=130°,
∴∠BAC+∠ACB=130°,
∴∠ABC=180°-(∠BAC+∠ACB)=50°;
(2)证明:连接OD,
∵BD平分∠ABC,
∴$\widehat{AD}$=$\widehat{CD}$,
∴OD⊥AC,
∵EF∥AC,
∴OD⊥EF,
∴直线EF是⊙O的切线.
点评 此题考查了切线的性质、垂径定理以及圆周角定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
16.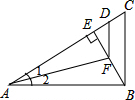 如图:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
如图:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
 如图:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
如图:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )| A. | ∠1=∠EFD | B. | BE=EC | C. | BF=CD | D. | FD∥BC |
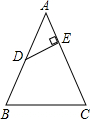 如图在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,求
如图在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,求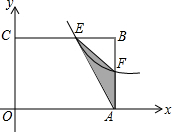 如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$的图象与BC边交于点E.