题目内容
9.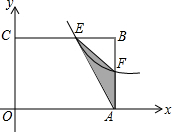 如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
分析 (1)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;
(2)根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.
解答 解:(1)∵在矩形OABC中,OA=3,OC=2,
∴B(3,2),
∵F为AB的中点,
∴F(3,1),
∵点F在反比例函数y=$\frac{k}{x}$的图象上,
∴k=3,
∴该函数的解析式为y=$\frac{3}{x}$;
(2)由题意知E,F两点坐标分别为E($\frac{k}{2}$,2),F(3,$\frac{k}{3}$),
∴S△EFA=$\frac{1}{2}$AF•BE=$\frac{1}{2}$×$\frac{1}{3}$k(3-$\frac{1}{2}$k),
=$\frac{1}{2}$k-$\frac{1}{12}$k2
=-$\frac{1}{12}$(k2-6k+9-9)
=-$\frac{1}{12}$(k-3)2+$\frac{3}{4}$
当k=3时,S有最大值.
S最大值=$\frac{3}{4}$.
点评 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定反比例解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 +7x2y2)÷(-7x2y)=
+7x2y2)÷(-7x2y)=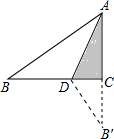 如图所示,在△ABC中,AB=10,AC=6,BC=8,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.
如图所示,在△ABC中,AB=10,AC=6,BC=8,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.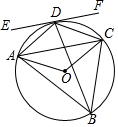 如图,⊙O是△ABC的外接圆,连接OA,OC,BD平分∠ABC,交⊙O于点D,连接AD,CD,过点D作直线EF∥AC,已知∠BDC+∠ACB=130°.
如图,⊙O是△ABC的外接圆,连接OA,OC,BD平分∠ABC,交⊙O于点D,连接AD,CD,过点D作直线EF∥AC,已知∠BDC+∠ACB=130°.