题目内容
2.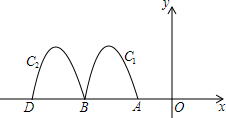 如图,抛物线y=-2x2-8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向左平移得C2,C2与x轴交于点B,D.若直线y=-x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2-8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向左平移得C2,C2与x轴交于点B,D.若直线y=-x+m与C1,C2共有3个不同的交点,则m的取值范围是( )| A. | -3<m<-$\frac{15}{8}$ | B. | $-3<m<-\frac{7}{4}$ | C. | -2<m<$\frac{1}{8}$ | D. | -3<m<-2 |
分析 首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=x+m与抛物线C2相切时m的值以及直线y=x+m过点B时m的值,结合图形即可得到答案.
解答  解:令y=-2x2-8x-6=0,
解:令y=-2x2-8x-6=0,
即x2+4x+3=0,
解得x=-1或-3,
则点A(-1,0),B(-3,0),
由于将C1向左平移2个长度单位得C2,
则C2解析式为y=-2(x+4)2+2(-5≤x≤-3),
当y=-x+m1与C2相切时,
令y=-x+m1=y=-2(x+4)2+2,
即2x2+15x+30+m1=0,
△=-8m1-15=0,
解得m1=-$\frac{15}{8}$,
当y=-x+m2过点B时,
即0=3+m2,
m2=-3,
当-3<m<-$\frac{15}{8}$时直线y=-x+m与C1、C2共有3个不同的交点,
故选:A.
点评 本题主要考查抛物线与x轴交点以及二次函数图象与几何变换的知识,解答本题的关键是正确地画出图形,利用数形结合进行解题,此题有一定的难度.

练习册系列答案
相关题目
12.下列说法中正确的是( )
| A. | -6既是负数、分数,也是有理数 | |
| B. | 0既不是正数、也不是负数,但是整数 | |
| C. | -200既是负数、也是整数,但不是有理数 | |
| D. | 以上都不正确 |
13. 如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任意作一条直线分别交AD,BC,于E,F,则阴影部分的面积是( )
如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任意作一条直线分别交AD,BC,于E,F,则阴影部分的面积是( )
 如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任意作一条直线分别交AD,BC,于E,F,则阴影部分的面积是( )
如图,已知面积为1的正方形ABCD的对角线相交于点O,过点O任意作一条直线分别交AD,BC,于E,F,则阴影部分的面积是( )| A. | 1 | B. | 0.5 | C. | 0.25 | D. | 无法确定 |
17.下列各式运算结果为正数的是( )
| A. | -3+7-5 | B. | (1-2)×3 | C. | -16÷(-3)2 | D. | -24×(-6) |
 如图,直线y=k(x-2)+k-1与x轴、y轴分别交于B、C两点,且$\frac{OB}{OC}$=$\frac{1}{2}$.
如图,直线y=k(x-2)+k-1与x轴、y轴分别交于B、C两点,且$\frac{OB}{OC}$=$\frac{1}{2}$. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF=48°.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF=48°.
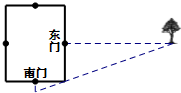 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”