题目内容
13．
如图，已知面积为1的正方形ABCD的对角线相交于点O，过点O任意作一条直线分别交AD，BC，于E，F，则阴影部分的面积是（ ）| A． | 1 | B． | 0.5 | C． | 0.25 | D． | 无法确定 |
分析 利用图形的全等的知识将分散的图形集中在一起，再结合图形的特征选择相应的公式求解．
解答 解：依据已知和正方形的性质及全等三角形的判定可知△AOE≌△COF，
则得图中阴影部分的面积为正方形面积的$\frac{1}{4}$，
因为正方形的边长为1，
则其面积为1，
于是这个图中阴影部分的面积为$\frac{1}{4}$．
故选C．
点评 本题综合考查了利用正方形的性质和全等三角形的判定的知识进行有关计算的能力，属于基础题．
练习册系列答案
相关题目
如图所示，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之积为24，则x+y=18．
4．
如图，抛物线与x轴的两个交点A（-3，0），B（1，0），则由图象可知y＜0时，x的取值范围是（ ）
如图，抛物线与x轴的两个交点A（-3，0），B（1，0），则由图象可知y＜0时，x的取值范围是（ ）| A． | -3＜x＜1 | B． | x＞1 | C． | x＜-3 | D． | 0＜x＜1 |
1．下列大小比较正确的是（ ）
| A． | -100＞0.01 | B． | -6＞-5 | C． | -1＞-2 | D． | -0.1＞0 |
2．
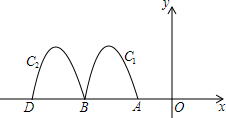如图，抛物线y=-2x2-8x-6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C1向左平移得C2，C2与x轴交于点B，D．若直线y=-x+m与C1，C2共有3个不同的交点，则m的取值范围是（ ）
如图，抛物线y=-2x2-8x-6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C1向左平移得C2，C2与x轴交于点B，D．若直线y=-x+m与C1，C2共有3个不同的交点，则m的取值范围是（ ）| A． | -3＜m＜-$\frac{15}{8}$ | B． | $-3＜m＜-\frac{7}{4}$ | C． | -2＜m＜$\frac{1}{8}$ | D． | -3＜m＜-2 |