题目内容
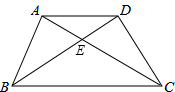 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.(1)求证:
| AB |
| AE |
| AC |
| AD |
(2)如果AB⊥AC,AE:EC=1:2,求证:AC=BD.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)利用相似三角形的判定得出△ABE∽△ACB,进而求出答案;
(2)在Rt△ABC中利用边长求得∠ACB=30°,进而得出AD∥BC,进一步可得到AE=DE,BE=CE,利用线段的和差可得出结论.
(2)在Rt△ABC中利用边长求得∠ACB=30°,进而得出AD∥BC,进一步可得到AE=DE,BE=CE,利用线段的和差可得出结论.
解答:证明:(1)∵AB=AD,
∴∠ADB=∠ABE,
又∵∠ADB=∠ACB,
∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,
∴△ABE∽△ACB,
∴
=
,
又∵AB=AD,
∴
=
;
(2)设AE=x,
∵AE:EC=1:2,
∴EC=2x,
由(1)得:AB2=AE•AC,
∴AB=
x,
又∵BA⊥AC,
∴BC=2
x,
∴∠ACB=30°,
又∵∠ADB=∠ACB=∠ABD,
∴∠ADB=∠ACB=∠CBD=30°,
∴AD∥BC,
∴∠DAC=∠ACB=30°,
∴BE=CE,AE=DE,
∴AE+CE=BE+DE,
即AC=BD.
∴∠ADB=∠ABE,
又∵∠ADB=∠ACB,
∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,
∴△ABE∽△ACB,
∴
| AB |
| AE |
| AC |
| AB |
又∵AB=AD,
∴
| AB |
| AE |
| AC |
| AD |
(2)设AE=x,
∵AE:EC=1:2,
∴EC=2x,
由(1)得:AB2=AE•AC,
∴AB=
| 3 |
又∵BA⊥AC,
∴BC=2
| 3 |
∴∠ACB=30°,
又∵∠ADB=∠ACB=∠ABD,
∴∠ADB=∠ACB=∠CBD=30°,
∴AD∥BC,
∴∠DAC=∠ACB=30°,
∴BE=CE,AE=DE,
∴AE+CE=BE+DE,
即AC=BD.
点评:此题主要考查了相似三角形的判定与性质,得出△ABE∽△ACB是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
若m是方程x2-2014x-1=0的根,则(m2-2014m+3)(m2-2014m+4)的值为( )
| A、16 | B、12 | C、20 | D、30 |
 +(4y2-3xy),其中x=-1,y=-
+(4y2-3xy),其中x=-1,y=-