题目内容
12. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
分析 (1)求出x=0时y的值与y=0时x的值即可得答案;
(2)分m>0和m<0两种情况,结合函数图象可得.
解答 解:(1)由题意,当x=0时,y=2.
∴A(0,2).
∵y=mx2-2mx+2=m(x-1)2+2-m,
∴对称轴为直线x=1.
∴B(1,0).
(2)由题意,C(-1,0),D(3,0).
①当m>0时,
结合函数图象可知,满足题意的抛物线的顶点须在x轴下方,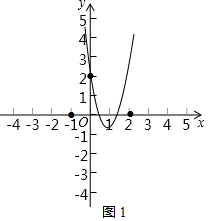
即2-m<0.
∴m>2.
②当m<0时,
过C(-1,0)的抛物线的顶点为E(1,$\frac{8}{3}$).
结合函数图象可知,满足条件的抛物线的顶点须在点E上方或与点E重合,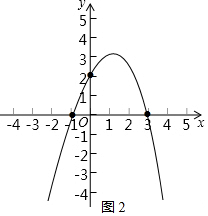
即2-m≥$\frac{8}{3}$.
∴m≤$-\frac{2}{3}$.
综上所述,m的取值范围为m>2或m≤$-\frac{2}{3}$.
点评 本题主要考查抛物线与x轴的交点,熟练掌握二次函数的图象与性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.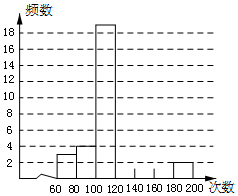 校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
176 118 94 144 102 92 113 105 108 60
115 104 126 158 105 132 114 118 152 104
151 165 102 132 112 114 118 114 168 172
105 118 68 126 128 139 84 136 76 145
134 128 126 110 96 148 146 156 186 182
(1)以20为组距,补充并完成频数分布表;
(2)请补充未完成的频数直方分布图;
(3)若该校七年级有300名学生,请估计60秒能跳绳120次以上的学生有多少人?
 校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:
校学生会体育干部想了解七年级学生60秒跳绳的情况,从七年级随机抽取了50名同学的成绩,统计如下:176 118 94 144 102 92 113 105 108 60
115 104 126 158 105 132 114 118 152 104
151 165 102 132 112 114 118 114 168 172
105 118 68 126 128 139 84 136 76 145
134 128 126 110 96 148 146 156 186 182
(1)以20为组距,补充并完成频数分布表;
(2)请补充未完成的频数直方分布图;
| 次数分组 | 频数 |
| 60≤x<80 | 3 |
| 80≤x<100 | 4 |
| 100≤x<120 | 19 |
| 120≤x<140 | 10 |
| 140≤x<160 | 8 |
| 160≤x<180 | 4 |
| 180≤x<200 | 2 |
| 合计 | 50 |
3.下列调查中,适合普查方式的是( )
| A. | 调查市场上老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了违禁品 | |
| D. | 调查某市初中生的睡眠情况 |
20.以下各数中比0小的是( )
| A. | -2 | B. | $\frac{3}{2}$ | C. | 0.5 | D. | 1 |
1.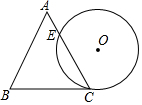 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则弧CE的长为( )| A. | 4cm | B. | 3cm | C. | $\frac{2\sqrt{3}π}{3}$cm | D. | $\frac{\sqrt{3}π}{3}$cm |
2.估计$\sqrt{41}$-2的值( )
| A. | 在4和5之间 | B. | 在3和4之间 | C. | 在2和3之间 | D. | 在1和2之间 |




