题目内容
20.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F.(1)求证:AH=BD;
(2)设BD=x,BE•BF=y,求y关于x的函数关系式;
(3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度.

分析 (1)由AD⊥BC,BH⊥AO,利用垂直的定义得到一对直角相等,再由一对公共角,且半径相等,利用AAS得到三角形ADO与三角形BHO全等,利用全等三角形对应边相等得到OH=OD,利用等式的性质化简即可得证;
(2)连接AB,AF,如图1所示,利用HL得到直角三角形ADB与直角三角形BHA全等,利用全等三角形对应角相等得到一对角相等,再由公共角相等得到三角形ABE与三角形AFB相似,由相似得比例即可确定出y与x的函数解析式;
(3)连接OF,如图2所示,利用两对角相等的三角形相似得到三角形AFO与三角形FOG相似,由相似得比例求出BD的长即可.
解答 (1)证明:∵AD⊥BC,BH⊥AO,
∴∠ADO=∠BHO=90°,
在△ADO与△BHO中,
$\left\{\begin{array}{l}∠ADO=∠BHO\\∠AOD=∠BOH\\ OA=OB\end{array}\right.$,
∴△ADO≌△BHO(AAS),
∴OH=OD,
又∵OA=OB,
∴AH=BD;
(2)解:连接AB、AF,如图1所示,
∵AO是半径,AO⊥弦BF,
∴∴AB=AF,
∴∠ABF=∠AFB,
在Rt△ADB与Rt△BHA中,
$\left\{\begin{array}{l}AH=BD\\ AB=BA\end{array}\right.$,
∴Rt△ADB≌Rt△BHA(HL),
∴∠ABF=∠BAD,
∴∠BAD=∠AFB,
又∵∠ABF=∠EBA,
∴△BEA∽△BAF,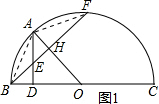
∴$\frac{BE}{BA}$=$\frac{BA}{BF}$,
∴BA2=BE•BF,
∵BE•BF=y,
∴y=BA2,
∵∠ADO=∠ADB=90°,
∴AD2=AO2-DO2,AD2=AB2-BD2,
∴AO2-DO2=AB2-BD2,
∵直径BC=8,BD=x,
∴AB2=8x,
则y=8x(0<x<4);
方法二:∵BE•BF=y,BF=2BH,
∴BE•BH=$\frac{1}{2}$y,
∵△BED∽△BOH,
∴$\frac{BE}{OB}$=$\frac{BD}{BH}$,
∴OB•BD=BE•BH,
∴4x=$\frac{1}{2}$y,
∴y=8x(0<x<4);
(3)解:连接OF,如图2所示,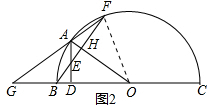
∵∠GFB是公共角,∠FAE>∠G,
∴当△FAE∽△FBG时,∠AEF=∠G,
∵∠BHA=∠ADO=90°,
∴∠AEF+∠DAO=90°,∠AOD+∠DAO=90°,
∴∠AEF=∠AOD,
∴∠G=∠AOD,
∴AG=AO=4,
∵∴∠AOD=∠AOF,
∴∠G=∠AOF,
又∵∠GFO是公共角,
∴△FAO∽△FOG,
∴$\frac{AF}{OF}$=$\frac{OF}{FG}$,
∵AB2=8x,AB=AF,
∴AF=2$\sqrt{2}$x,
∴$\frac{2\sqrt{2}x}{4}$=$\frac{4}{4+2\sqrt{2}x}$,
解得:x=3±$\sqrt{5}$,
∵3+$\sqrt{5}$>4,舍去,
∴BD=3-$\sqrt{5}$.
点评 此题属于圆的综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,圆周角定理,熟练掌握判定与性质是解本题的关键.

| A. | -3.1×10-4 | B. | 3.1×10-6 | C. | -0.31×10-5 | D. | -3.1×10-6 |
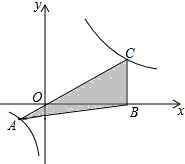 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}(x<0)$图象上一点,AO的延长线交函数y=$\frac{{k}^{2}}{x}(x>0,k>0)$的图象交于点C,CB⊥x轴,若△ABC的面积等于6,则k的值是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
| A. | 37×104 | B. | 3.7×104 | C. | 37×105 | D. | 3.7×105 |
| A. | a≥2 | B. | a>2 | C. | a≠2 | D. | a≠-2 |