题目内容
1.在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm,以点C为圆心,r为半径作⊙C(1)若直线AB与⊙C没有公共点,求r的取值范围;
(2)若边AB与⊙C有两个公共点,求r的取值范围;
(3)若边AB与⊙C只有一个公共点,求r的取值范围.
分析 过C作CD⊥AB于D,根据勾股定理得到AB=5cm,根据三角形的面积公式得到CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$cm,然后根据圆心到AB的距离与半径的关系即可得到结论.
解答 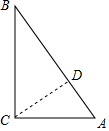 解:过C作CD⊥AB于D,
解:过C作CD⊥AB于D,
∵∠C=90°,BC=4cm,AC=3cm,
∴AB=5cm,
∴CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$cm,
(1)若直线AB与⊙C没有公共点,r的取值范围是0<r<$\frac{12}{5}$;
(2)若边AB与⊙C有两个公共点,r的取值范围是r>$\frac{12}{5}$;
(3)若边AB与⊙C只有一个公共点,r的取值范围是r=$\frac{12}{5}$.
点评 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
9.下列方程中是二元一次方程的是( )
| A. | 4y2-3x=28 | B. | y=5x | C. | 2x=8 | D. | x2-y=12 |
 由10块相同的小长方形地砖拼成面积为1.6m2的长方形ABCD(如图),则长方形ABCD的周长为5.2m.
由10块相同的小长方形地砖拼成面积为1.6m2的长方形ABCD(如图),则长方形ABCD的周长为5.2m.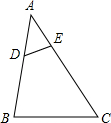 如图,在△ABC中,∠A=55°,D,E分别是AB,AC上的点,则∠B,∠C,∠ADE与∠AED的度数和为250°.
如图,在△ABC中,∠A=55°,D,E分别是AB,AC上的点,则∠B,∠C,∠ADE与∠AED的度数和为250°.