题目内容
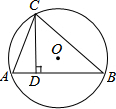 如图,△ABC内接于⊙O,CD是△ABC的高,CD=6,AD=3,BD=8,求⊙O的面积.
如图,△ABC内接于⊙O,CD是△ABC的高,CD=6,AD=3,BD=8,求⊙O的面积.考点:垂径定理,勾股定理
专题:
分析:如图,作辅助线,首先证明△CAD∽△CEB,进而得到CE=
;运用勾股定理求出AC、BC的长度即可解决问题.
| CA•CB |
| CD |
解答: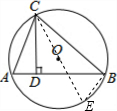 解:如图,作直径CE,连接BE;
解:如图,作直径CE,连接BE;
则∠CBE=90°;
∵CD⊥AB,
∴∠CDA=90°;
又∵∠A=∠E,
∴△CAD∽△CEB,
∴
=
,
∴CE=
;
由勾股定理得:
AC2=62+32=45,BC2=82+62=100,
∴AC=3
,BC=10,
∴CE=
=5
,
∴⊙O的半径r=
,
∴⊙O的面积=π•(
)2=
.
 解:如图,作直径CE,连接BE;
解:如图,作直径CE,连接BE;则∠CBE=90°;
∵CD⊥AB,
∴∠CDA=90°;
又∵∠A=∠E,
∴△CAD∽△CEB,
∴
| CA |
| CE |
| CD |
| CB |
∴CE=
| CA•CB |
| CD |
由勾股定理得:
AC2=62+32=45,BC2=82+62=100,
∴AC=3
| 5 |
∴CE=
3
| ||
| 6 |
| 5 |
∴⊙O的半径r=
5
| ||
| 2 |
∴⊙O的面积=π•(
5
| ||
| 2 |
| 125π |
| 4 |
点评:该命题以圆为载体,以圆周角定理及其推论、勾股定理的应用为考查的核心构造而成;同时还渗透了对相似三角形的判定及其应用等几何知识点的考查;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列说法正确的是( )
| A、符号不同的两个数互为相反数 |
| B、倒数等于本身的数是0,1,-1 |
| C、平方等于9的数是3 |
| D、负数的偶次幂是正数 |
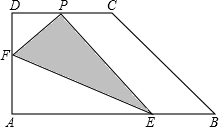 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于