题目内容
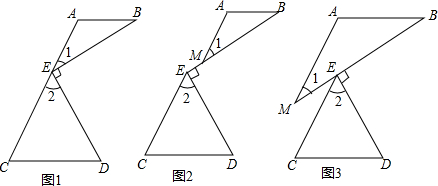
19.(1)已知:如图1,BE⊥DE,∠1=∠B,∠2=∠D,试证明AB与CD平行.(2)若图形变化为如图2、图3所示,且满足AB∥CD,BE⊥DE,∠1=∠B,∠2=∠D,那么∠1与∠2有怎样的关系?选择一个图形进行证明.
分析 (1)过点E作EN∥AB,根据平行线的性质得到∠BEN=∠B,等量代换得到∠BEN=∠1,推出∠D=∠DEN,
根据平行线的判定即可得到结论;
(2)如答图2,过点E作EN∥AB,根据平行线的性质得到∠B=∠1,量代换得到∠BEN=∠1,推出EN∥CD,于是得到结论.
解答 解:(1)过点E作EN∥AB,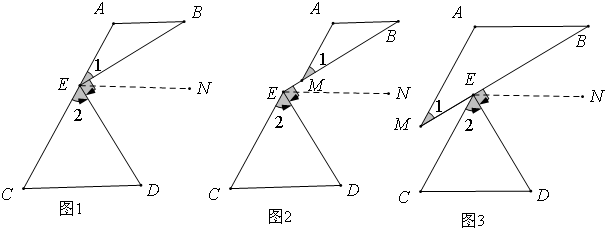
则∠BEN=∠B,∵∠1=∠B,
∴∠BEN=∠1,
∵∠BEN+∠DEN=∠BED=90°,
∴∠1+∠2=90°,
∴∠2=∠DEN,
∵∠2=∠D,
∴∠D=∠DEN,
∴AB∥CD;
(2)如答图2,过点E作EN∥AB,
∴∠BEN=∠B,
∵∠B=∠1,
∴∠BEN=∠1,
∵∠BED=90°=∠BEN+∠DEN,∠1+∠2=90°,
∴∠DEN=∠2,
∵∠2=∠D,
∴EN∥CD,
∴AB∥CD.
点评 本题考查了平行线的判定和性质,关键是掌握平行线的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列叙述正确的是( )
| A. | 有两条边对应相等的两个直角三角形一定全等 | |
| B. | 两个等边三角形一定全等 | |
| C. | 有一条边对应相等的两个等腰三角形一定全等 | |
| D. | 面积相等的两个三角形一定全等 |