题目内容
4.计算:-22÷(3-$\frac{1}{2}$)-(2-4).分析 原式先计算乘方运算,再计算除法运算,最后算加减运算即可得到结果.
解答 解:原式=-4÷$\frac{5}{2}$-(-2)=-$\frac{8}{5}$+2=$\frac{2}{5}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
14.阅读下列材料:
有这样一个问题:关于x 的一元二次方程a x2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:请将(2)补充完整
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程mx2-(2m+3)x-4m=0有一个负实根,一个正实根,且负实根大于-1,求实数m的取值范围.
有这样一个问题:关于x 的一元二次方程a x2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:请将(2)补充完整
| 方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
| 方程有两个 不相等的负实根 | 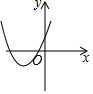 | $\left\{\begin{array}{l}a>0\\△={b^2}-4ac>0\\-\frac{b}{2a}<0\\ c>0.\end{array}\right.$ |
| 方程有一个负实根,一个正实根 | 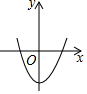 | $\left\{\begin{array}{l}a>0\\ c<0.\end{array}\right.$ |
| 方程有两个 不相等的正实根 | 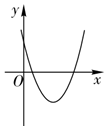 | $\left\{\begin{array}{l}a>0\\△={b^2}-4ac>0\\-\frac{b}{2a}>0\\ c>0.\end{array}\right.$ |
(2)若一元二次方程mx2-(2m+3)x-4m=0有一个负实根,一个正实根,且负实根大于-1,求实数m的取值范围.
15. 如图所示,数轴上点A、B对应的有理数分别为a、b,下列说法正确的是( )
如图所示,数轴上点A、B对应的有理数分别为a、b,下列说法正确的是( )
 如图所示,数轴上点A、B对应的有理数分别为a、b,下列说法正确的是( )
如图所示,数轴上点A、B对应的有理数分别为a、b,下列说法正确的是( )| A. | ab>0 | B. | a+b>0 | C. | |a|-|b|<0 | D. | a-b<0 |
9.用四舍五入法,分别按要求取0.05026的近似值,下列四个结果中错误的是( )
| A. | 0.1(精确到0.1) | B. | 0.05(精确到0.01) | ||
| C. | 0.05(精确到0.001) | D. | 0.0503(精确到0.0001) |
14.下列各图案中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
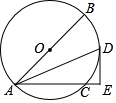 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD. 如图,已知∠AOD:∠BOD=1:3,OC是∠AOD的平分线.若∠AOB=120°,求:
如图,已知∠AOD:∠BOD=1:3,OC是∠AOD的平分线.若∠AOB=120°,求: