题目内容
20.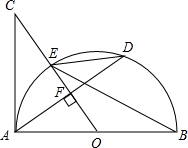 如图,AB是半圆O的直径,过点O作弦AD的垂线,垂足为F,交半圆O于点E,交AC于点C,使∠BED=∠C.
如图,AB是半圆O的直径,过点O作弦AD的垂线,垂足为F,交半圆O于点E,交AC于点C,使∠BED=∠C.(1)判断直线AC与⊙O的位置关系,并证明你的结论;
(2)若AC=10,cos∠BED=$\frac{4}{5}$,求AD的长.
分析 (1)先证∠BAD+∠AOF=90°,再由圆周角定理和已知条件找出∠BAD=∠C,得出∠C+∠AOF=90°,从而证出AC⊥OA,得出结论;
(2)先由三角函数求出CF,再由勾股定理求出AF,然后由垂径定理即可得出结果.
解答 解:(1)直线AC是⊙O的切线;理由如下:
∵OE⊥AD,
∴∠AFO=90°,
∴∠BAD+∠AOF=90°,
∵∠BED=∠C,∠BED=∠BAD,
∴∠BAD=∠C,
∴∠C+∠AOF=90°,
∴∠OAC=90°,即AC⊥OA,
∴直线AC是⊙O的切线;
(2)∵cos∠BED=$\frac{4}{5}$,
∴cos∠C=$\frac{CF}{AC}$=$\frac{4}{5}$,
∴CF=AC•$\frac{4}{5}$=10×$\frac{4}{5}$=8,
∴AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵OE⊥AD,
∴AF=$\frac{1}{2}$AD,
∴AD=2AF=12.
点评 本题考查了切线的判定、锐角三角函数、勾股定理的运用;熟练掌握切线的判定方法,运用锐角三角函数进行计算是解决问题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
11.已知二次函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
| A. | k<4 | B. | k≤4 | C. | k>4 | D. | k≤4且k≠3 |
8.下列解方程变形过程正确的是( )
| A. | 由2x-1=3得2x=2 | B. | 由-3(x+4)=5得-3x-4=5 | ||
| C. | 由2(x-1)=4得x-1=2 | D. | 由-4x=5得x=-$\frac{4}{5}$ |
15.-0.5的相反数是( )
| A. | 2 | B. | -2 | C. | -0.5 | D. | 0.5 |
10.若式子$\frac{x}{2x-y}$中的x、y都扩大2倍,则分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 扩大3倍 | D. | 不确定 |
 已知线段a、b,用圆规和直尺画线段,使它等于2a+b.(简要写出画法,保留作图痕迹)
已知线段a、b,用圆规和直尺画线段,使它等于2a+b.(简要写出画法,保留作图痕迹)