题目内容
3.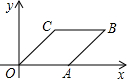 如图,菱形OABC在平面直角坐标系中的位置如图所示,若sin∠AOC=$\frac{3}{5}$,OA=5,则点B的坐标为( )
如图,菱形OABC在平面直角坐标系中的位置如图所示,若sin∠AOC=$\frac{3}{5}$,OA=5,则点B的坐标为( )| A. | (4,3) | B. | (3,4) | C. | (9,3) | D. | (8,4) |
分析 过点B作BD⊥x轴于D,根据菱形的性质可得AB=OA,AB∥OC,根据两直线平行,同位角相等可得∠BAD=∠AOC,然后求出BD,再利用勾股定理列式求出AD,从而得到OD,最后写出点B的坐标即可.
解答  解:如图,过点B作BD⊥x轴于D,
解:如图,过点B作BD⊥x轴于D,
∵四边形OABC是菱形,
∴AB=OA=5,AB∥OC,
∴∠BAD=∠AOC,
∵sin∠AOC=$\frac{3}{5}$,
∴BD=AB×sin∠AOC=5×$\frac{3}{5}$=3,
由勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴OD=OA+AD=5+4=9,
∴点B的坐标为(9,3).
故选C.
点评 本题考查了菱形的性质,坐标与图形性质,解直角三角形,熟记性质并作辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
13.在算式(-2)□(+3)的□中填上运算符号,使结果最小,运算符号是( )
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
14.一组数据2,0,-2,1,3的平均数是( )
| A. | 2 | B. | 1.5 | C. | 1 | D. | 0.8 |
18.下列数据:11,12,13,10,13的中位数和众数分别为( )
| A. | 10和11 | B. | 11和12 | C. | 12和13 | D. | 11和13 |
8.下列计算中,正确的是( )
| A. | $\sqrt{5}-\sqrt{4}=1$ | B. | $\sqrt{8}•\sqrt{2}=4$ | C. | $\sqrt{a^2}=a$ | D. | $\frac{{\sqrt{6}}}{3}=\sqrt{2}$ |
12.已知直角三角形的外接圆半径为6,内切圆半径为2,那么这个三角形的面积是( )
| A. | 32 | B. | 34 | C. | 27 | D. | 28 |
 如图,点A在双曲线y=$\frac{k}{x}$的图象上,AB⊥x轴于B,且△AOB的面积为2,则k的值为( )
如图,点A在双曲线y=$\frac{k}{x}$的图象上,AB⊥x轴于B,且△AOB的面积为2,则k的值为( )