题目内容
12.已知直角三角形的外接圆半径为6,内切圆半径为2,那么这个三角形的面积是( )| A. | 32 | B. | 34 | C. | 27 | D. | 28 |
分析 如图,点O是△ABC的外心,点D是△ABC的内心,E、F、M是△ABCD 内切圆与△ABC的切点.设AB=a,BC=b,则有2=$\frac{a+b-12}{2}$,推出a+b=16,所以a2+2ab+b2=256,因为a2+b2=122=144,推出2ab=112,推出$\frac{1}{2}$ab=28,由此即可解决问题.
解答 解:如图,点O是△ABC的外心,点D是△ABC的内心,E、F、M是△ABCD 内切圆与△ABC的切点.
设AB=a,BC=b,则有2=$\frac{a+b-12}{2}$,
∴a+b=16,
∴a2+2ab+b2=256,
∵a2+b2=122=144,
∴2ab=112,
∴$\frac{1}{2}$ab=28.
∴△ABC的面积为28.
故选D.
点评 本题考查三角形内切圆与内心、外接圆与外心等知识,解题的关键是记住直角三角形的内切圆半径r=$\frac{a+b-c}{2}$,学会利用参数解决问题,属于中考选择题中的压轴题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
3.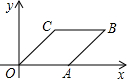 如图,菱形OABC在平面直角坐标系中的位置如图所示,若sin∠AOC=$\frac{3}{5}$,OA=5,则点B的坐标为( )
如图,菱形OABC在平面直角坐标系中的位置如图所示,若sin∠AOC=$\frac{3}{5}$,OA=5,则点B的坐标为( )
 如图,菱形OABC在平面直角坐标系中的位置如图所示,若sin∠AOC=$\frac{3}{5}$,OA=5,则点B的坐标为( )
如图,菱形OABC在平面直角坐标系中的位置如图所示,若sin∠AOC=$\frac{3}{5}$,OA=5,则点B的坐标为( )| A. | (4,3) | B. | (3,4) | C. | (9,3) | D. | (8,4) |
20. 如图,AB∥CD,且∠ACB=90°,则与∠CAB互余的角有( )个.
如图,AB∥CD,且∠ACB=90°,则与∠CAB互余的角有( )个.
 如图,AB∥CD,且∠ACB=90°,则与∠CAB互余的角有( )个.
如图,AB∥CD,且∠ACB=90°,则与∠CAB互余的角有( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 |
7.关于x的方程(k-3)x2+2x+1=0有实数根,则k的取值范围为( )
| A. | k≥4 | B. | k≤4且k≠3 | C. | k<4 | D. | k≤4 |
4.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.已知x1,x2是一元二次方程x2-6x+4=0的两根,则x1x2的值是( )
| A. | -2 | B. | 1 | C. | 4 | D. | -4 |
2.解方程$\frac{x-4}{2}$-$\frac{1+2x}{4}$=1时,去分母正确的是( )
| A. | 2(x-4)-(1+2x)=1 | B. | 4(x-4)2 (1+2x)=4 | C. | 2 (x-4)-1+2x=4 | D. | 2(x-4)一-(1+2x)=4 |