题目内容
14．写出一个开口向下，经过点（0，3）的抛物线的表达式y=-x2+x+3（答案不唯一）．分析 根据a确定抛物线开口方向，图象过（0，3）可得c=3，进而得出答案．
解答 解：由题意可得：a＜0，c=3，
符合题意的解析式可以为：y=-x2+x+3（答案不唯一）．
故答案为：y=-x2+x+3（答案不唯一）．
点评 此题主要考查了二次函数的性质，正确得出a，c的值是解题关键．
练习册系列答案
相关题目
4．一个三位数，百位上的数字是a，十位上的数字是a的2倍，个位上的数字比十位上的数字小1，这个三位数用代数式可以表示为（ ）
| A． | 122a-1 | B． | 113a-1 | C． | 5a-1 | D． | 111a-1 |
5．下列方程是一元二次方程的是（ ）
| A． | ax2+bx+c=0 | B． | 3x2-2x=3（x2-2） | C． | x3-2x-4=0 | D． | （x-1）2-1=0 |
9．
如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC．下列比例式正确的是（ ）
如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC．下列比例式正确的是（ ）| A． | $\frac{AD}{DB}$=$\frac{CE}{AE}$ | B． | $\frac{AD}{DB}$=$\frac{AE}{AC}$ | C． | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | D． | $\frac{AD}{AB}$=$\frac{EC}{AE}$ |
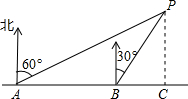如图，小明同学在东西方向的环海路A处，测得海中灯塔P在它的北偏东60°方向上，在A的正东200米的B处，测得海中灯塔P在它的北偏东30°方向上．问：灯塔P到环海路的距离PC约等于多少米？（$\sqrt{3}$取1.732，结果精确到1米）
6．已知二次函数y=2（x+1）（x-a），其中a＞0，且对称轴为直线x=2，则a的值是（ ）
| A． | 3 | B． | 5 | C． | 7 | D． | 不确定 |
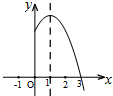已知二次函数y=-2x2+4x+m的部分图象如图所示，则关于x的一元二次方程-2x2+4x+m=0的解是x1=-1，x2=3．