题目内容
4．
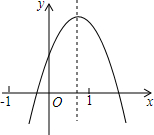已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0；②2a+b＜0；③4a-2b+c＜0；④b2-4ac＞0，其中正确结论的个数为（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
分析 根据图象的开口可确定a．再结合对称轴，可确定b，根据图象与y轴的交点位置，可确定c，根据图象与x轴的交点个数可确定△．
解答 解：∵图象开口向下，
∴a＜0，
∵x=-$\frac{b}{2a}$＞0，
∴b＞0，
∵图象与y轴的正半轴相交，
∴c＞0，
∴abc＜0，故①错误；
∵抛物线的对称轴x=-$\frac{b}{2a}$＜1，a＜0，
∴b＜-2a，
∴2a+b＜0，故②正确；
∵当x=-2时，y＜0，
∴4a-2b+c＜0，故③正确；
∵图象和x轴交于两点，
∴b2-4ac＞0，故④正确．
故选B．
点评 本题考查了二次函数的图象和系数的关系，解题的关键是熟练掌握二次函数的有关性质、以及二次函数的图象的特点．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
9．与$\sqrt{2}$是同类二次根式的为（ ）
| A． | $\sqrt{6}$ | B． | $\sqrt{8}$ | C． | $\sqrt{12}$ | D． | $\sqrt{24}$ |
如图，在△ABC中，DE∥BC，EF∥AB，若BD：DA=5：3，则CF：CB=5：8．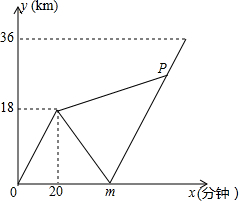
甲、乙两名大学生去距学校36千米的某乡镇进行社会调查，他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回，乙取相机后（在学校取相机所用时间忽略不计）骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为x（分钟）．y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：