题目内容
6. 如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.求证:
如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.求证:(1)∠PMN=∠PNM;
(2)BM=BN.
分析 (1)根据角平分线的性质得到PM=PN,根据等腰三角形的性质证明即可;
(2)根据同角的余角相等解出证明.
解答 证明:(1)∵PB是∠ABC的平分线,PM⊥AB,PN⊥BC,
∴PM=PN,
∴∠PMN=∠PNM;
(2)∵PM⊥AB,PN⊥BC,
∴∠PMB=∠PNB=90°,又∠PMN=∠PNM,
∴∠BMN=∠BNM,
∴BM=BN.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
 某计算程序编辑如图所示,当输入x=12或-$\frac{2}{3}$时,输出的y=3.
某计算程序编辑如图所示,当输入x=12或-$\frac{2}{3}$时,输出的y=3.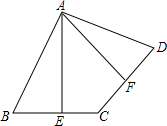 如图所示,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD,
如图所示,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD,
 如图,已知△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,点D为AB边上一点,且AD:BD=1:3,连接CD,现将CD绕点C顺时针旋转90°度得到线段CE,连接EB,则线段EB的长是5.
如图,已知△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,点D为AB边上一点,且AD:BD=1:3,连接CD,现将CD绕点C顺时针旋转90°度得到线段CE,连接EB,则线段EB的长是5.