题目内容
15. 如图,已知△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,点D为AB边上一点,且AD:BD=1:3,连接CD,现将CD绕点C顺时针旋转90°度得到线段CE,连接EB,则线段EB的长是5.
如图,已知△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,点D为AB边上一点,且AD:BD=1:3,连接CD,现将CD绕点C顺时针旋转90°度得到线段CE,连接EB,则线段EB的长是5.
分析 连结AE,如图,先判断△ACB为等腰直角三角形得到∠BAC=∠ABC=45°,AB=$\sqrt{2}$AC=4,则BD=3,再根据旋转的性质得CE=CD,∠DCE=90°,利用等角的余角相等得到∠ACE=∠BCD,则根据旋转的定义可判断△CBD绕点C顺时针旋转90°度得到△CAE,接着根据旋转的性质得AE=BD=3,∠CAE=∠CBD=45°,所以∠BAE=90°,最后在Rt△BAE中利用勾股定理可计算出EB的长.
解答 解:连结AE,如图,
∵∠ACB=90°,AC=BC=2$\sqrt{2}$,
∴△ACB为等腰直角三角形,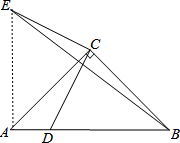
∴∠BAC=∠ABC=45°,AB=$\sqrt{2}$AC=4,
∵AD:BD=1:3,
∴BD=3,
∵CD绕点C顺时针旋转90°度得到线段CE,
∴CE=CD,∠DCE=90°,
∴∠ACE=∠BCD,
∴△CBD绕点C顺时针旋转90°度得到△CAE,
∴AE=BD=3,∠CAE=∠CBD=45°,
∴∠BAE=45°+45°=90°,
在Rt△BAE中,∵AE=3,AB=4,
∴BE=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为5.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.

练习册系列答案
相关题目
20.若a为实数,则下列说法正确的是( )
| A. | |-a|是正数 | B. | -|a|是负数 | C. | $\sqrt{{a}^{2}}$是非负数 | D. | |-a|永远大于-|a| |
 如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.求证:
如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.求证: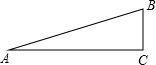 如图,在Rt△ABC中,∠C=90°,∠A=15°
如图,在Rt△ABC中,∠C=90°,∠A=15°