题目内容
1.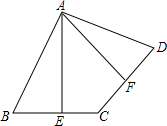 如图所示,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD,
如图所示,在四边形ABCD中,点E是BC的中点,点F是CD的中点,且AE⊥BC,AF⊥CD,(1)求证:AB=AD;
(2)请你探究,当AB与BC和CD之间有什么关系时,△AEF为等边三角形,并证明.
分析 (1)连接AC,由已知条件可得△ABC为等腰三角形;△ACD为等腰三角形,根据等腰三角形的性质:两腰相等即可证得AB=AD;
(2)连接EF,由△AEF为等边三角形,可得∠AEF=∠AFE=60°,易得EC=FC,利用全等三角形的判定定理可得Rt△AEC≌Rt△AFC,易得∠EAC=∠FAC=30°,由等腰三角形的性质可得∠BAE=∠CAE=∠FAC=∠FAD=30°,易得△ABC与△ADC均为等边三角形,得出结论.
解答  (1)证明:连接AC,
(1)证明:连接AC,
∵点E是BC的中点,且AE⊥BC,
∴△ABC为等腰三角形,
∴AB=AC,
同理可得:AC=AD,
∴AB=AD;
(2)解: 当AB=BC=CD时,△AEF为等边三角形;
当AB=BC=CD时,△AEF为等边三角形;
连接EF,
∵△AEF为等边三角形,
∴∠AEF=∠AFE=60°,
∴∠FEC=∠EFC=30°,
∴EC=FC,
在Rt△AEC与Rt△AFC中,
$\left\{\begin{array}{l}{AC=AC}\\{EC=FC}\end{array}\right.$,
∴Rt△AEC≌Rt△AFC,
∴∠EAC=∠FAC=30°,
∵△ABC与△ADC均为等腰三角形,AE⊥BC,AF⊥CD,
∴∠BAE=∠CAE=∠FAC=∠FAD=30°,
∴∠BAC=60°,
∴△ABC与△ADC均为等边三角形,
∴AB=BC=CD,
∴当AB=BC=CD时,△AEF为等边三角形.
点评 本题考查了等腰三角形和全等三角形及等边三角形的判定和性质定理,作出恰当的辅助线构建全等三角形是解答此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12.下面正确的命题中,其逆命题不成立的是( )
| A. | 对顶角相等 | |
| B. | 角平分线上的点到这个角的两边的距离相等 | |
| C. | 全等三角形的对应边相等 | |
| D. | 同旁内角互补,两直线平行 |
9.下列各数是负数的是( )
| A. | 20 | B. | -21 | C. | $\frac{11}{7}$ | D. | 0 |
 如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.求证:
如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.求证: