如图.在△ABC中.AB=AC.∠BAC=100°.AB的垂直平分线DE分别交AB.BC于点D.E.则∠BAE=( )A．80°B．60°C．50°D．40° 题目和参考答案——青夏教育精英家教网—

题目内容

12．

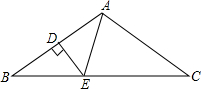如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（　　）

A．

80°

B．

60°

C．

50°

D．

40°

分析首先利用三角形的内角和定理和等腰三角形的性质∠B，利用线段垂直平分线的性质易得AE=BE，∠BAE=∠B．

解答解：∵AB=AC，∠BAC=100°，
∴∠B=∠C=（180°-100°）÷2=40°，
∵DE是AB的垂直平分线，
∴AE=BE，
∴∠BAE=∠B=40°，
故选D．

点评本题主要考查了等腰三角形的性质，三角形的内角和定理，线段垂直平分线的性质，掌握垂直平分线上任意一点，到线段两端点的距离相等和等边对等角是解答此题的关键．

练习册系列答案

相关题目

2．

如图，直线y=$\frac{1}{2}$x+2交x轴、y轴于A、B两点，点C与点A关于y轴对称，点D是线段AB上一个动点，ED=EC，且sin∠EDC=$\frac{\sqrt{5}}{5}$．
（1）求证：△DEC∽△ABC；
（2）求证：BE∥AC；
（3）若D在直线AB上运动时，是否存在这样的点D使△DEC的面积最小？如果存在请求出D点的坐标和△DEC面积的最小值；如果不存在，请说明理由．

3．

如图，已知扇形AOB中，OA=10cm，∠AOB=36°．
（1）求扇形AOB的面积；
（2）将扇形AOB绕B点顺时针方向旋转，得一新扇形A′O′B，其中A点在O′B上，如图所示，求O点旋转至O′点所经过的路径的长．

20．

在平面直角坐标系xOy中，过点（0，2）且平行于x轴的直线，与直线y=x-1交于点A，点A关于直线x=1的对称点为B，抛物线C₁：y=x²+bx+c经过点A，B．
（1）求点A，B的坐标；
（2）求抛物线C₁的表达式及顶点坐标；
（3）若抛物线C₂：y=ax²（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围．

7．

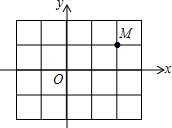如图，在平面直角坐标系中，将点M（2，1）向下平移2个单位长度得到点N，则点N的坐标为（　　）

17．（1）计算：-（-2）+（1+π）⁰-|-$\sqrt{2}$|+$\sqrt{8}$；
（2）先化简，再求值：（x+2）（x-2）-x（x+3），其中x=-3．

4．如图1，抛物线y=-x²+2x+3与x轴交于A，B，与y轴交于C，抛物线的顶点为D，直线l过C交x轴于E（4，0）．
（1）写出D的坐标和直线l的解析式；
（2）P（x，y）是线段BD上的动点（不与B，D重合），PF⊥x轴于F，设四边形OFPC的面积为S，求S与x之间的函数关系式，并求S的最大值；
（3）点Q在x轴的正半轴上运动，过Q作y轴的平行线，交直线l于M，交抛物线于N，连接CN，将△CMN沿CN翻转，M的对应点为M′．在图2中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．

1．一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是（　　）

	A．	至少有1个球是黑球		B．	至少有1个球是白球
	C．	至少有2个球是黑球		D．	至少有2个球是白球

2．

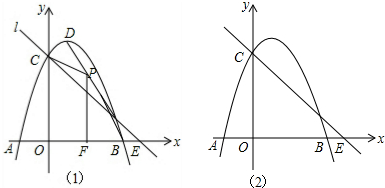
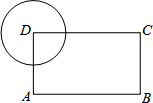如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是3＜r＜5．

试题分类