Question

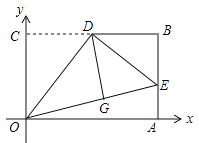
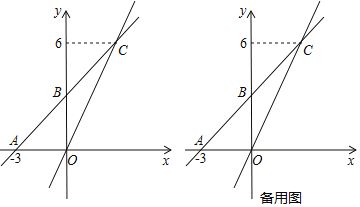
【题目】如图，在△ABC中，AB=AC=10，∠B=30°，O是线段AB上的一个动点，以O为圆心，OB为半径作⊙O交BC于点D，过点D作直线AC的垂线，垂足为E．

（1）求证：DE是⊙O的切线；

（2）设OB=x，求∠ODE的内部与△ABC重合部分的面积y的最大值．

Answer 1

【答案】（1）证明见解析；

（2）①当x=时，S△ODF最大，最大值为；②当x=6时，重合部分的面积最大，最大值为10．

【解析】试题分析：（1）由等腰三角形的性质可得∠C=∠B，∠ODB=∠C，从而∠ODB=∠C，根据同位角相等两直线平行可证OD∥AC，进而可证明结论；（2）①当点E在CA的延长线上时，设DE与AB交于点F，围成的图形为△ODF; ②当点E在线段AC上时，围成的图形为梯形AODE.根据三角形和梯形的面积公式列出函数关系式，利用二次函数的性质求解.

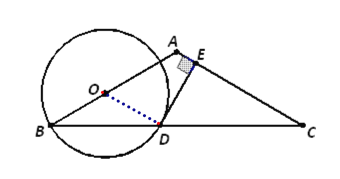
证明：（1）连接OD，

∵AB=AC，

∴∠C=∠B．

∵OB=OD，

∴∠ODB=∠B

∴∠ODB=∠C

∴OD∥AC．

∵DE⊥AC，

∴OD⊥DE，

∴DE是⊙O的切线．

（2）①当点E在CA的延长线上时，设DE与AB交于点F，围成的图形为△ODF．

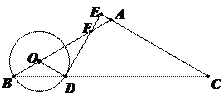
∵OD= OB= x，∠B=30°，∴∠FOD=60°，

∵∠ODE=90°，∴DF= x，

∴S△ODF= x·x= x，(0＜x≤)

当x=时，S△ODF最大，最大值为；

②当点E在线段AC上时，围成的图形为梯形AODE．

∵AB=AC=10，∠B=30°，∴BC=10，

作OH⊥BC，∵OD= OB= x，∠B=30°，

∴BD= 2BH= x，∴CD= 10x，

∵∠C=30°，∠DEC=90°，

∴DE= (10－x)，CE= (10－x)=15－x，∴AE=x－5，

∴S梯形AODE= (x－5+ x)· (10－x)= (－x+12 x－20) (＜x＜10)

当x=6时，S梯形AODE最大，最大值为10；

综上所述，当x=6时，重合部分的面积最大，最大值为10．