题目内容
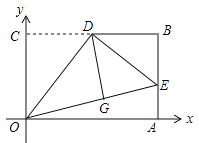
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=![]() ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
【答案】(![]() ,
,![]() ).
).
【解析】
试题分析:过点G作GF⊥OA于点F,如图所示.
∵点D为BC的中点,∴DC=DB=DG,∵四边形OABC是矩形,∴AB=OC,OA=BC,∠C=∠OGD=∠ABC=90°.
在Rt△DGE和Rt△DBE中,∵DB=DG,DE=DE,∴Rt△DGE≌Rt△DBE(HL),∴BE=GE.
设AE=a,则BE=3﹣a,DE=![]() =
=![]() ,OG=OC=3,∴OE=OG++GE,即
,OG=OC=3,∴OE=OG++GE,即![]() =3+3﹣a,解得:a=1,∴AE=1,OE=5.∵GF⊥OA,EA⊥OA,∴GF∥EA,∴
=3+3﹣a,解得:a=1,∴AE=1,OE=5.∵GF⊥OA,EA⊥OA,∴GF∥EA,∴![]() ,∴OF=
,∴OF=![]() =
=![]() =
=![]() ,GF=
,GF=![]() =
=![]() =
=![]() ,∴点G的坐标为(
,∴点G的坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).


练习册系列答案
相关题目