Question

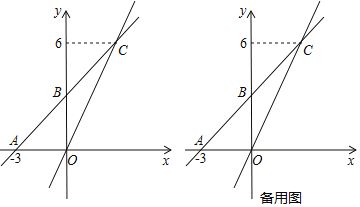
【题目】如图，在平面直角坐标系中，一次函数的图象与轴交于点，与轴交于点，且与正比例函数的图象交于点.

（1）求一次函数的解析式；

（2）点在轴上，当最小时，求出点的坐标；

（3）若点是直线上一点，点是平面内一点，以、、、四点为顶点的四边形是矩形，请直接写出点的坐标.

Answer 1

【答案】（1）；（2）；（3）或（，）.

【解析】

（1）由A、C坐标，利用待定系数法可求得答案；

（2）由一次函数解析式可求得B点坐标，可求得B点关于x轴的对称点B′的坐标，连接B′C与x轴的交点即为所求的P点，由B′、C坐标可求得直线B′C的解析式，则可求得P点坐标；

（3）分两种情形分别讨论：①当OC为边时，四边形OCFE是矩形，此时EO⊥OC；②当OC为对角线时，四边形OE′CF′是矩形，此时OE′⊥AC；分别求出E和E’的坐标，然后根据矩形的性质和坐标间的位置关系即可得到点的坐标.

解：（1）∵一次函数y＝mx＋n（m≠0）的图象经过点A（3，0），点C（3，6），

∴，解得，

∴一次函数的解析式为y＝x＋3；

（2）如图，作点B关于x轴的对称点B′，连接CB′交x轴于P，此时PB＋PC的值最小．

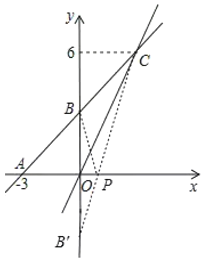
∵B（0，3），C（3，6）

∴B′（0，-3），

设直线CB′的解析式为y=kx+b（k≠0），

则，解得：，

∴直线CB′的解析式为y＝3x3，

令y＝0，得x＝1，

∴P（1，0）；

（3）如图，

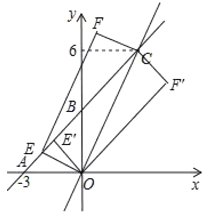
①当OC为边时，四边形OCFE是矩形，此时EO⊥OC，

∵直线OC的解析式为y＝2x，

∴直线OE的解析式为y＝x，

联立，解得，

∴E（2，1），

∵EO＝CF，OE∥CF，

根据坐标之间的位置关系易得：F（1，7）；

②当OC为对角线时，四边形OE′CF′是矩形，此时OE′⊥AC，

∴直线OE′的解析式为y＝x，

由，解得，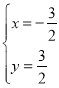

∴E′（，），

∵OE′＝CF′，OE′∥CF′，

根据坐标之间的位置关系易得：F′（，），

综上所述，满足条件的点F的坐标为（1，7）或（，）．