题目内容
先阅读材料,然后解答问题:
要把多项式am+an+bm+bn因式分解,可以先把它的前两项分成一组,并提出a,再把它的后两项分成一组,并提出b,从而得到a(m+n)+b(m+n),这时,由于a(m+n)与b(m+n)又有公因式(m+n),于是可提出公因式(m+n),从而得到(m+n)(a+b),即
am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b).
这种因式分解的方法叫做分组分解法.请利用分组分解法把下列多项式进行因式分解:
m3-2m2-4m+8.
要把多项式am+an+bm+bn因式分解,可以先把它的前两项分成一组,并提出a,再把它的后两项分成一组,并提出b,从而得到a(m+n)+b(m+n),这时,由于a(m+n)与b(m+n)又有公因式(m+n),于是可提出公因式(m+n),从而得到(m+n)(a+b),即
am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b).
这种因式分解的方法叫做分组分解法.请利用分组分解法把下列多项式进行因式分解:
m3-2m2-4m+8.
考点:因式分解-分组分解法
专题:阅读型
分析:原式两项两项结合后,提取公因式,再利用平方差公式分解即可.
解答:解:原式=(m3-2m2)-(4m-8)
=m2(m-2)-4(m-2)
=(m+2)(m-2)2.
=m2(m-2)-4(m-2)
=(m+2)(m-2)2.
点评:此题考查了因式分解-分组分解法,难点是采用两两分组还是三一分组.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
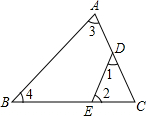 如图,点D,E在△ABC的边上,∠C=50°,则∠1+∠2+∠3+∠4的度数为( )
如图,点D,E在△ABC的边上,∠C=50°,则∠1+∠2+∠3+∠4的度数为( )| A、130° | B、260° |
| C、280° | D、360° |
下列方程中,是一元一次方程的是( )
| A、x2-4x=3 | ||
B、x-1=
| ||
| C、x+2y=3 | ||
| D、x=0 |
在下列有理数中,正有理数是( )
| A、0 |
| B、-8 |
| C、(-3)2 |
| D、-|-2| |
 如图,∠A+∠B+∠D+∠E+∠F+∠G=
如图,∠A+∠B+∠D+∠E+∠F+∠G=