题目内容
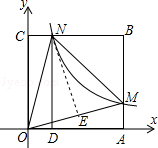
 如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=
如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:
分析:由反比例函数y=
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,易证得CN=AM,即可得△OAN≌△OAM,可得ON=OM,然后设作NE⊥OM于E点,易得△ONE为等腰直角三角形,设NE=x,则ON=
x,由勾股定理可求得x的值,继而可设正方形ABCO的边长为a,则OC=a,CN=a-
,则可得到点N的坐标,继而求得答案.
| k |
| x |
| 2 |
| 2 |
解答:解:∵点M、N都在y=
的图象上,
∴S△ONC=S△OAM=
k,即
OC•NC=
OA•AM,
∵四边形ABCO为正方形,
∴OC=OA,∠OCN=∠OAM=90°,
∴NC=AM,
在△OCN和△OAM中,
,
∴△OCN≌△OAM(SAS);
∴ON=OM,
作NE⊥OM于E点,如图,
∵∠MON=45°,
∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则ON=
x,
∴OM=
x,
∴EM=
x-x=(
-1)x,
在Rt△NEM中,MN=2,
∵MN2=NE2+EM2,即22=x2+[(
-1)x]2,
∴x2=2+
,
∴ON2=(
x)2=4+2
,
∵CN=AM,CB=AB,
∴BN=BM,
∴△BMN为等腰直角三角形,
∴BN=
MN=
,
设正方形ABCO的边长为a,则OC=a,CN=a-
,
∵在Rt△OCN中,OC2+CN2=ON2,
∴a2+(a-
)2=4+2
,
解得a1=
+1,a2=-1(舍去),
∴OC=
+1,
∴BC=OC=
+1,
∴CN=BC-BN=1,
∴N点坐标为(1,
+1),
将点N代入反比例函数y=
,得:k=
+1,
∴反比例函数的解析式为:y=
.
故答案为:y=
.
| k |
| x |
∴S△ONC=S△OAM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABCO为正方形,
∴OC=OA,∠OCN=∠OAM=90°,
∴NC=AM,
在△OCN和△OAM中,
|
∴△OCN≌△OAM(SAS);
∴ON=OM,
作NE⊥OM于E点,如图,
∵∠MON=45°,
∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则ON=
| 2 |
∴OM=
| 2 |
∴EM=
| 2 |
| 2 |
在Rt△NEM中,MN=2,
∵MN2=NE2+EM2,即22=x2+[(
| 2 |
∴x2=2+
| 2 |

∴ON2=(
| 2 |
| 2 |
∵CN=AM,CB=AB,
∴BN=BM,
∴△BMN为等腰直角三角形,
∴BN=
| ||
| 2 |
| 2 |
设正方形ABCO的边长为a,则OC=a,CN=a-
| 2 |
∵在Rt△OCN中,OC2+CN2=ON2,
∴a2+(a-
| 2 |
| 2 |
解得a1=
| 2 |
∴OC=
| 2 |
∴BC=OC=
| 2 |
∴CN=BC-BN=1,
∴N点坐标为(1,
| 2 |
将点N代入反比例函数y=
| k |
| x |
| 2 |
∴反比例函数的解析式为:y=
| ||
| x |
故答案为:y=
| ||
| x |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、比例系数的几何意义和正方形的性质;熟练运用勾股定理和等腰直角三角形的性质进行几何计算.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
一个三角形分别为8,15,17,这个三角形最长边上的高是( )
A、
| ||
B、7
| ||
C、8
| ||
| D、8 |

 如图直线AB与CD相交于点O,OP是∠BOC的平分线,OF⊥CD,∠AOD=40°∠COP的度数是
如图直线AB与CD相交于点O,OP是∠BOC的平分线,OF⊥CD,∠AOD=40°∠COP的度数是