题目内容
13. 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD=( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 求出∠BCD=∠A=30°,根据含30°角的直角三角形性质得出BC=$\frac{1}{2}$AB,BD=$\frac{1}{2}$BC,代入求出即可.
解答 解:∴CD是高,
∴∠BDC=90°,
∵∠ACB=90°,∠A=30°,
∴∠B=60°,BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
∴∠BCD=30°,
∴BD=$\frac{1}{2}$BC=2,
故选A.
点评 本题考查了睡觉内角和定理,含30°角的直角三角形性质的应用,能根据含30°角的直角三角形性质得出BC=$\frac{1}{2}$AB和BD=$\frac{1}{2}$BC是解此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
12.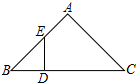 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )| A. | DE=DB | B. | DE=AE | C. | AE=BE | D. | AE=BD |
18.在实数$\sqrt{2}$,π,0.52$\stackrel{•}{5}$,$\sqrt{9}$,0.7070070007…、(每两个“7”之间依次多一个“0”)中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列方程是一元二次方程的是( )
| A. | $\sqrt{x+1}$ | B. | 2x(x-1)=2x2+3 | C. | $3x+\frac{1}{x}=4$ | D. | x2-2=0 |
2.下列长度的三条线段能组成三角形的是( )
| A. | 1,2,3 | B. | 20,15,8 | C. | 4,5,9 | D. | 5,15,8 |
3.能分解成(x+2)(y-3)的多项式是( )
| A. | xy-2x+3y-6 | B. | xy-3y+2x-y | C. | -6+2y-3x+xy | D. | -6+2x-3y+xy |
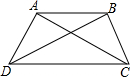 如图,AD=BC,∠ADC=∠BCD,求证:∠BAC=∠ABD.
如图,AD=BC,∠ADC=∠BCD,求证:∠BAC=∠ABD.