题目内容
 梯形ABCD中,AD∥BC,请用尺规作图并解决问题.
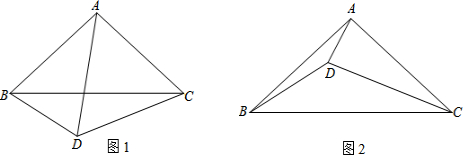
梯形ABCD中,AD∥BC,请用尺规作图并解决问题.(1)作AB中点E,连接DE并延长交射线CB于点F,在DF的下方作∠FDG=∠ADE,边DG交BC于点G,连接EG;
(2)试判断EG与DF的位置关系,并说明理由.
考点:作图—复杂作图,全等三角形的判定与性质,梯形
专题:
分析:(1)作出线段AB的垂直平分线,进而得出AB的中点E,再作∠FDG=∠ADE,求出即可;
(2)首先得出△ADE≌△BFE(AAS),进而求出EF=DE,利用等腰三角形的性质得出答案.
(2)首先得出△ADE≌△BFE(AAS),进而求出EF=DE,利用等腰三角形的性质得出答案.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)∵AD∥BC,
∴∠ADE=∠F,
在△ADE和△BFE中,
∴△ADE≌△BFE(AAS),
∴EF=DE,
又∵∠ADE=∠FDG,
∴∠F=∠FDG,
∴DG=FG,
∴EG⊥DF.
 解:(1)如图所示:
解:(1)如图所示:(2)∵AD∥BC,
∴∠ADE=∠F,
在△ADE和△BFE中,
|
∴△ADE≌△BFE(AAS),
∴EF=DE,
又∵∠ADE=∠FDG,
∴∠F=∠FDG,
∴DG=FG,
∴EG⊥DF.
点评:此题主要考查了复杂作图、全等三角形的判定与性质以及梯形的性质和等腰三角形的性质等知识,熟练掌握等腰三角形的性质是解题关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列从左到右的变形属于因式分解的是( )
| A、x2-2xy+y2=x(x-2y)+y2 |
| B、x2-16y2=(x+8y)(x-8y) |
| C、x2+xy+y2=(x+y)2 |
| D、x4y4-1=(x2y2+1)(xy+1)(xy-1) |
已知关于x,y的方程组
,给出下列结论:
①
是方程组的解;
②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4-a的解;
④x,y的都为自然数的解有4对.
其中正确的个数为( )
|
①
|
②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4-a的解;
④x,y的都为自然数的解有4对.
其中正确的个数为( )
| A、3个 | B、2个 | C、1个 | D、4个 |
下列说法错误的是( )
| A、平行四边形的对角相等 |
| B、平行四边形的对角互补 |
| C、平行四边形的对边相等 |
| D、平行四边形的内角和是360° |

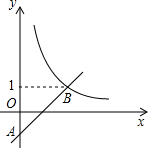 如图,在平面直角坐标系中,一次函数y=ax-a(a为常数)的图象与y轴相交于点A,与函数
如图,在平面直角坐标系中,一次函数y=ax-a(a为常数)的图象与y轴相交于点A,与函数