Question

如图，把同样大小的黑色棋子摆放在正多边形的边上．

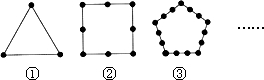
第4个图形需要

 

个棋子．按照这样的规律摆下去，则第n（n为正整数）个图形需要黑色棋子的个数是

 

个．（用含n的代数式表示）

Answer 1

考点：规律型：图形的变化类

专题：

分析：结合图形，发现：第1个图形中的棋子数是2×3-3=1×3=3（个）；第2个图形中的棋子数是3×4-4=2×4=8（个）；第3个图形中的棋子数是4×5-5=3×5=15（个），…以此类推，则第n（n是正整数）个图形需要黑色棋子的个数是n（n+2）个．

解答：解：第1个图形中的棋子数是2×3-3=1×3=3（个）；
第2个图形中的棋子数是3×4-4=2×4=8（个）；
第3个图形中的棋子数是4×5-5=3×5=15（个），
第4个图形中的棋子数是5×6-6=4×6=24（个），
…
第n个图形中的棋子数是n（n+2）个．
故答案为：24；n（n+2）．

点评：此题主要考查了图形的变化类，根据多边形的周长的方法进行计算，注意每个顶点的重复．