题目内容
 如图,点D,E在△ABC的内部,且BE平分∠ABD,CE平分∠ACD,若∠A=α,∠BDC=β,则∠BEC等于
如图,点D,E在△ABC的内部,且BE平分∠ABD,CE平分∠ACD,若∠A=α,∠BDC=β,则∠BEC等于考点:三角形内角和定理
专题:
分析:结合图形可得∠BDC=∠ABD+∠A+∠ACD,代入∠A=α,∠BDC=β即可得到∠ABD+∠ACD的值,再利用上面得出的结论可知∠BEC=
(∠ABD+∠ACD)+∠A,易得答案.
| 1 |
| 2 |
解答:解:∵BE平分∠ABD,CE平分∠ACD,
∴∠ABE=
∠ABD,∠ACE=
∠ACD,
∠BEC=∠ABE+∠ACE+∠A=
(∠ABD+∠ACD)+∠A=
(β-α)+α=
(α+β).
故答案为:
(α+β).
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∠BEC=∠ABE+∠ACE+∠A=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查三角形外内角和定理,解答的关键是沟熟知三角形的内角和等于180°的知识点.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
下列计算错误的是( )
| A、0-(-5)=5 | ||||||
| B、(-3)-(-5)=2 | ||||||
C、
| ||||||
| D、(-36)÷(-9)=-4 |
 根据三角形外心的概念,我们可引入下一个新定义:
根据三角形外心的概念,我们可引入下一个新定义: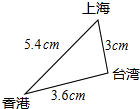 在中国地图册上,联结上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示.飞机从台湾直飞上海的距离约为l290千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是
在中国地图册上,联结上海、香港、台湾三地构成一个三角形,用刻度尺测得它们之间的距离如图所示.飞机从台湾直飞上海的距离约为l290千米,那么飞机从台湾绕道香港再到上海的空中飞行距离是
 在一个边长为4cm正方形里作一个扇形(如图所示),再将这个扇形剪下卷成一个圆锥的侧面,则这个圆锥的高为
在一个边长为4cm正方形里作一个扇形(如图所示),再将这个扇形剪下卷成一个圆锥的侧面,则这个圆锥的高为