题目内容
16.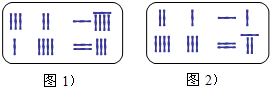 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )| A. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{4x+3y=27}\end{array}\right.$ |
分析 由图1可得1个竖直的算筹数算1,一个横的算筹数算10,每一横行是一个方程,第一个数是x的系数,第二个数是y的系数,第三个数是相加的结果:前面的表示十位,后面的表示个位,由此可得图2的表达式.
解答 解:第一个方程x的系数为2,y的系数为1,相加的结果为11;第二个方程x的系数为4,y的系数为3,相加的结果为27,所以可列方程为$\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$.
故选:A.
点评 本题主要考查的是列二元一次方程组,读懂图意,得到所给未知数的系数及相加结果是解题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
6.若a+b=3,a-b=$\frac{1}{3}$,则a2-b2的值为( )
| A. | 1 | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | 9 |
 如图,直线AB与CD相交于点O,E是∠AOD内一点,已知OE⊥CD,∠AOE=40°,则∠BOD=50°.
如图,直线AB与CD相交于点O,E是∠AOD内一点,已知OE⊥CD,∠AOE=40°,则∠BOD=50°.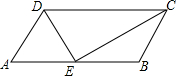 已知,如图,在平行四边形ABCD中,AB=2AD,E为AB的中点,连接DE,EC,求证:DE⊥EC.
已知,如图,在平行四边形ABCD中,AB=2AD,E为AB的中点,连接DE,EC,求证:DE⊥EC.