题目内容
某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=
,月销售量y3(件)与销售月份x(月)满足y3=10x+20.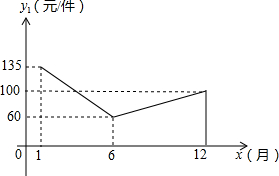
(1)根据图象求出销售价格y1(元/件)与销售月份x(月)之间的函数关系式;(6≤x≤12且x为整数)
(2)求出该服装月销售利润W(元)与月份x(月)之间的函数关系式,并求出哪个月份的销售利润最大?最大利润是多少?(6≤x≤12且x为整数)
|

(1)根据图象求出销售价格y1(元/件)与销售月份x(月)之间的函数关系式;(6≤x≤12且x为整数)
(2)求出该服装月销售利润W(元)与月份x(月)之间的函数关系式,并求出哪个月份的销售利润最大?最大利润是多少?(6≤x≤12且x为整数)
考点:二次函数的应用
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)根据销售额减去销售成本,可得销售利润,根据函数的性质,可得最大利润.
(2)根据销售额减去销售成本,可得销售利润,根据函数的性质,可得最大利润.
解答:解:(1)设销售价格y1(元/件)与销售月份x(月)之间的函数关系式为y1=kx+b (6≤x≤12),
函数图象过(6,60)、(12,100),则
,
解得
.
故销售价格y1(元/件)与销售月份x(月)之间的函数关系式y1=
x+20 (6≤x≤12且x为整数);
(2)由题意得w=y1•y3-y2•y3即
w=(
x+20)•(10x+20)-
x•(10x+20)
化简,得
w=20x2+240x+400,
∵a=20,x=-
=-
=-6是对称轴,
当x>-6时,w随x的增大而增大,
∴当x=12时,销售量最大,W最大=20×122+240×12+400=6160,
答:12月份利润最大,最大利润是6160元.
函数图象过(6,60)、(12,100),则
|
解得
|
故销售价格y1(元/件)与销售月份x(月)之间的函数关系式y1=
| 20 |
| 3 |
(2)由题意得w=y1•y3-y2•y3即
w=(
| 20 |
| 3 |
| 14 |
| 3 |
化简,得
w=20x2+240x+400,
∵a=20,x=-
| b |
| 2a |
| 240 |
| 2×20 |
当x>-6时,w随x的增大而增大,
∴当x=12时,销售量最大,W最大=20×122+240×12+400=6160,
答:12月份利润最大,最大利润是6160元.
点评:本题考查了二次函数的应用,利用了待定系数法求解析式,利用了函数的减区间求函数的最大值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
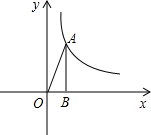 如图,点A在双曲线y=
如图,点A在双曲线y= 如图,在4×4正方形网格中,每个小正方形的边长都为1.
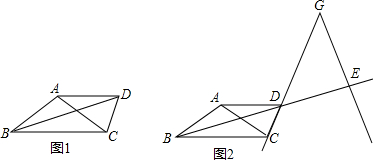
如图,在4×4正方形网格中,每个小正方形的边长都为1. 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.