题目内容
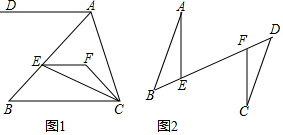
14．
如果小球在如图所示的七巧板上自由滚动，并随机停留在这七巧板的某个位置上（不考虑停在边线的情况），那么它最终停留在△CDE的概率是$\frac{1}{8}$．
分析 直接利用七巧板得出各边长之间的关系，再利用三角形面积求法结合概率公式得出答案．
解答 解：由题意可得：DE=$\frac{1}{2}$DF，CD=$\frac{1}{2}$BD，
故△CDE的面积=四边形ABDF的面积×$\frac{1}{8}$，
故最终停留在△CDE的概率是：$\frac{1}{8}$．
故答案为：$\frac{1}{8}$．
点评 此题主要考查了几何概率以及七巧板，正确得出各边之间的关系是解题关键．
练习册系列答案
相关题目
2．关于直线l：y=kx+k（k≠0），下列说法不正确的是（ ）
| A． | 点（0，k）在直线l上 | B． | 直线l经过定点（-1，0） | ||
| C． | 直线l经过第一、二、三象限 | D． | 当k＞0时，y随x的增大而增大 |
6．把根式-a$\sqrt{-\frac{1}{a}}$化成最简二次根式为（ ）
| A． | $\sqrt{-a}$ | B． | $a\sqrt{-a}$ | C． | $-\sqrt{-a}$ | D． | -$a\sqrt{-a}$ |