题目内容
9.(1)如图1,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.(2)如图2,AB∥CD,AB=CD,BF=DE,求证:∠AEF=∠CFB.
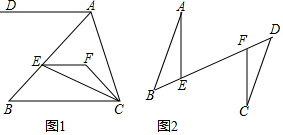
分析 (1)推出EF∥BC,根据平行线性质求出∠ACB,求出∠FCB,根据角平分线求出∠ECB,根据平行线的性质推出∠FEC=∠ECB,代入即可.
(2)根据平行线的性质、线段间的和差关系证得∠B=∠D、BE=DF;然后由全等三角形的判定定理SAS推知△ABE≌△CDF;最后由全等三角形的对应角相等证得结论;
解答 解:(1)∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB-∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
(2)∵AB∥CD(已知),
∴∠B=∠D,
又∵BF=DE,
∴BF-EF=DE-EF,即BE=DF,
∴在△ABE和△CDF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠B=∠D}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴∠A=∠C,
∴∠BEA=∠DFC,
∴:∠AEF=∠CFB.
点评 本题考查了平行线的性质和判定,平行公理及推论,全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若x1,x2,…,x10的平均数是10,x11,x12,…,x30的平均数是20,则x1,x2,…x30的平均数是( )
| A. | 10 | B. | 20 | C. | 15 | D. | $\frac{50}{3}$ |
18.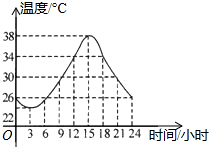 如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )
如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )
 如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )
如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )| A. | 这天15点时温度最高 | |
| B. | 这天3点时温度最低 | |
| C. | 这天最高温度与最低温度的差是16℃ | |
| D. | 这天1点时温度是30℃ |
19.多项式2a2b-πab2-ab的项数及次数分别为( )
| A. | 3,4 | B. | 3,3 | C. | 3,2 | D. | 2,3 |
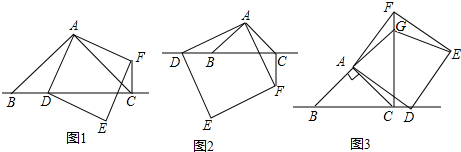
 如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在△CDE的概率是$\frac{1}{8}$.
如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在△CDE的概率是$\frac{1}{8}$.