题目内容
14.有下列命题:①两条直线被第三条直线所截,同位角相等;
②0.1 的算术平方根是0.01;
③算术平方根等于它本身的数是1;
④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;
⑤若a2=b2,则a=b;
⑥若$\root{3}{a}$=$\root{3}{b}$,则a=b.
其中假命题的个数是( )
| A. | 3个 | B. | 4 个 | C. | 5个 | D. | 6个 |
分析 利用平行线的性质、算术平方根的定义、点的坐标等知识分别判断后即可确定假命题的个数.
解答 解:①两条平行直线被第三条直线所截,同位角相等,故错误,是假命题;
②0.1 的算术平方根是0.01,错误,是假命题;
③算术平方根等于它本身的数是1和0,故错误,是假命题;
④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1或-2,故错误,是假命题;
⑤若a2=b2,则a=±b,故错误,是假命题;
⑥若$\root{3}{a}$=$\root{3}{b}$,则a=b,正确,是真命题,
假命题有5个,故选C.
点评 此题考查了命题与定理的知识,解题的关键是了解平行线的性质、算术平方根的定义、点的坐标等知识,难度不大.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19.下列各数中,互为相反数的是( )
| A. | -2与(-2)2 | B. | -2与2 | C. | -2与-$\frac{1}{2}$ | D. | $\frac{1}{2}$与-2 |
6.已知正n边形的一个内角为144°,则边数n的值是( )
| A. | 10 | B. | 9 | C. | 8 | D. | 6 |
3.$\sqrt{3-m}$的相反数为( )
| A. | -$\sqrt{3-m}$ | B. | $\sqrt{m-3}$ | C. | $\sqrt{3-m}$ | D. | $\frac{\sqrt{3-m}}{3-m}$ |
4.点M(3,-4)关于y的轴的对称点是M1,则M1关于x轴的对称点M2的坐标为( )
| A. | (-3,4) | B. | (-3,-4) | C. | (3,4) | D. | (3,-4) |
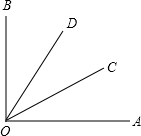 如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.
如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.
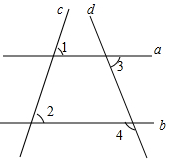 直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于110°.
直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于110°.