题目内容
已知⊙O是△ABC的外接圆,OD⊥BC且交BC于点D,∠BOD=40°,则∠BAC= .
考点:圆周角定理,垂径定理
专题:
分析:首先根据题意画出图形,利用圆周角定理,即可求得∠BAC的度数,注意分别从△ABC是锐角三角形或钝角三角形去分析求解即可求得答案.
解答: 解:如图,连接OC,
解:如图,连接OC,
∵OD⊥BC,OB=OC,
∵∠BOD=40°,
∴∠BOC=2∠BOD=80°,
∴当△ABC是锐角三角新时,∠BAC=
∠BOC=40°,
当△ABC是钝角三角形时,∠BA′C=180°-∠BAC=140°,
∴∠BAC=40°或140°.
故答案为:40°或140°.
 解:如图,连接OC,
解:如图,连接OC,∵OD⊥BC,OB=OC,
∵∠BOD=40°,
∴∠BOC=2∠BOD=80°,
∴当△ABC是锐角三角新时,∠BAC=
| 1 |
| 2 |
当△ABC是钝角三角形时,∠BA′C=180°-∠BAC=140°,
∴∠BAC=40°或140°.
故答案为:40°或140°.
点评:此题考查了圆周角定理以及等腰三角形的性质.此题比较简单,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
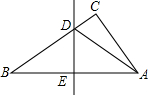 如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,BD=5cm,则△ABD的周长是( )
如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,BD=5cm,则△ABD的周长是( )| A、8cm | B、11cm |
| C、13cm | D、16cm |
已知代数式
x2y5与-3x2y2k-1是同类项,那么k的值是( )
| 1 |
| 2 |
| A、2 | B、3 | C、-2 | D、-3 |
 活动楼梯如图所示,∠B=90°,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为
活动楼梯如图所示,∠B=90°,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为 如图,⊙O的直径CD与弦AB垂直相交于点E,且BC=1,AD=2,求⊙O的直径长.
如图,⊙O的直径CD与弦AB垂直相交于点E,且BC=1,AD=2,求⊙O的直径长. 如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数为
如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数为