题目内容
 活动楼梯如图所示,∠B=90°,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为
活动楼梯如图所示,∠B=90°,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为考点:解直角三角形的应用-坡度坡角问题
专题:
分析:根据铅直高度:水平宽度=1:1,可用未知数表示出铅直高度和水平宽度的值,进而可用勾股定理求得铅直高度的值.
解答: 解:如图.AC=8米,BC:AB=1:1.
解:如图.AC=8米,BC:AB=1:1.
设BC=x米,则AB=x米.
在Rt△ABC中,AC2=BC2+AB2,
即x2+x2=82,
解得x=4
,
即BC=4
米.
故上升高度是4
米.
故答案为:4
.
 解:如图.AC=8米,BC:AB=1:1.
解:如图.AC=8米,BC:AB=1:1.设BC=x米,则AB=x米.
在Rt△ABC中,AC2=BC2+AB2,
即x2+x2=82,
解得x=4
| 2 |
即BC=4
| 2 |
故上升高度是4
| 2 |
故答案为:4
| 2 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了坡度的定义以及直角三角形中三角函数值的计算.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
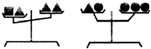 设“▲”、“■”和“●”分别表示三种不同的物体,现用同一天平秤两次,
设“▲”、“■”和“●”分别表示三种不同的物体,现用同一天平秤两次,如图,那么▲、■、●三种物质按质量从小到大排列应该是( )
| A、■●▲ | B、▲■● |
| C、■▲● | D、●▲■ |
已知⊙O的直径为13cm,如果直线和圆心的距离为7.5cm,那么直线和圆的公共点的个数为( )
| A、1 | B、3 | C、2 | D、0 |
以下列各组数为边长,能构成直角三角形的是( )
| A、5,7,8 | ||||
| B、1,2,3 | ||||
C、
| ||||
D、
|
 作图:在数轴上找到表示实数-
作图:在数轴上找到表示实数-