题目内容
14.已知:$\frac{2cos60°}{5-2a}$=$\frac{1}{a-1}$,求代数式(1+$\frac{1}{a+1}$)÷$\frac{{a}^{2}+4a+4}{{a}^{2}-1}$的值(先化简,再求值)分析 先求出a的值,再根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:∵$\frac{2cos60°}{5-2a}$=$\frac{1}{a-1}$,
∴$\frac{1}{5-2a}$,解得a=2.
原式=$\frac{a+2}{a+1}$×$\frac{(a+1)(a-1)}{{(a+2)}^{2}}$
=$\frac{a-1}{a+2}$,
将a=2代入得,原式=$\frac{2-1}{2+1}$=$\frac{1}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.函数y=$\sqrt{1-x}$+$\frac{1}{x-1}$ 的自变量x的取值范围是( )
| A. | x<1 | B. | x≠1 | C. | x≤1 | D. | x<1或 x≠1 |
19. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
6.已知x=-1是一元二次方程x2+mx-1=0的一个根,则另一个根是( )
| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
3.若$\frac{3a}{3-a}$有意义,则$\frac{3a}{3-|a|}$( )
| A. | 无意义 | B. | 有意义 | C. | 值为0 | D. | 以上答案都不对 |
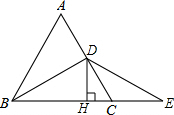 如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.
如图,在等腰△ABC中,AB=AC,BD为∠ABC平分线,延长BC到点E,使CE=CD,作DH⊥BE于H,求证:H为BE的中点.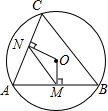 如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC垂足分别为M、N,如果MN=6,那么BC=12.
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC垂足分别为M、N,如果MN=6,那么BC=12. 如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则BE:DF等于8:1.
如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则BE:DF等于8:1.