题目内容
6. 如图,在矩形纸片ABCD中,BC=10,CD=8,如图,折叠纸片,试点A落在BC边上的A′处,折痕为PQ,当A′在BC上运动时,折痕的端点P,Q也随之移动.若限定Q只能在AD上移动,则线段PQ的最小值为5$\sqrt{5}$.
如图,在矩形纸片ABCD中,BC=10,CD=8,如图,折叠纸片,试点A落在BC边上的A′处,折痕为PQ,当A′在BC上运动时,折痕的端点P,Q也随之移动.若限定Q只能在AD上移动,则线段PQ的最小值为5$\sqrt{5}$.
分析 根据翻折变换,当点Q与点D重合时,点A′到达最左边,当点P与点B重合时,点A′到达最右边,所以点A′就在这两个点之间移动,分别求出这两个位置时PQ的长度,即可得到线段PQ的最小值为5$\sqrt{5}$.
解答  解:在矩形纸片ABCD中,BC=10,CD=8,
解:在矩形纸片ABCD中,BC=10,CD=8,
∴AB=CD=8,AD=BC=10,
如图1,当点D与点Q重合时,根据翻折对称性可得
A′D=AD=10,A′P=AP,
在Rt△A′CD中,A′C2=A′D2-CD2,
∴A′C=6,A′B=4,
在Rt△A′BP中,A′P2=PB2+A′B2,
∴A′P2=(8-A′P)2+42,
∴A′P=5,
∴PQ=$\sqrt{A′{P}^{2}+A′{D}^{2}}$=5$\sqrt{5}$
如图2,当点P与点B重合时,根据翻折对称性可得A′B=AB=8,
∴PQ=$\sqrt{A{B}^{2}+A{Q}^{2}}$=8$\sqrt{2}$,
∵5$\sqrt{5}$<8$\sqrt{2}$,
∴线段PQ的最小值为5$\sqrt{5}$,
故答案为:5$\sqrt{5}$.
点评 此题考查了折叠的性质、矩形的性质以及勾股定理,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
16.已知a+b=5,ab=4,则ab2+a2b-a-b的值是( )
| A. | -15 | B. | 15 | C. | 6 | D. | -6 |
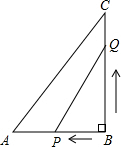 如图,在△ABC中,∠B=90°,AB=8cm,BC=12cm,点P从B点开始沿BA边向A以1cm/s的速度移动,点Q也从B点开始沿BC边向点C以2cm/s的速度移动,设运动时间为t秒.
如图,在△ABC中,∠B=90°,AB=8cm,BC=12cm,点P从B点开始沿BA边向A以1cm/s的速度移动,点Q也从B点开始沿BC边向点C以2cm/s的速度移动,设运动时间为t秒.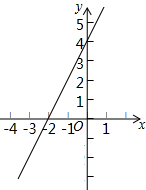 如图所示,直线l是一次函数的图象.
如图所示,直线l是一次函数的图象.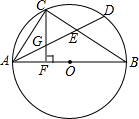 AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.
AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.