Question

20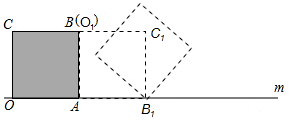．把边长为1的正方形纸片PABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处，又将正方形纸片AO₁C₁B₁绕B₁点，按顺时针方向旋转90°…，按上述方法经过2016次旋转后，顶点O经过的总路径的长为（252$\sqrt{2}$+504）π．

Answer 1

分析 为了便于标注字母，且更清晰的观察，每次旋转后向右稍微平移一点，作出前几次旋转后的图形，点O的第1次旋转路线是以正方形的边长为半径，以90°圆心角的扇形，第2次旋转路线是以正方形的对角线长为半径，以90°圆心角的扇形，第3次旋转路线是以正方形的边长为半径，以90°圆心角的扇形；
①根据弧长公式列式进行计算即可得解；
②求出2016次旋转中有几个4次，然后根据以上的结论进行计算即可求解．

解答 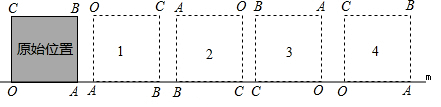解：如图，为了便于标注字母，且位置更清晰，每次旋转后不防向右移动一点，
第1次旋转路线是以正方形的边长为半径，以90°圆心角的扇形，路线长为$\frac{90π×1}{180}$=$\frac{1}{2}$π；
第2次旋转路线是以正方形的对角线长$\sqrt{2}$为半径，以90°圆心角的扇形，路线长为$\frac{90π×\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π；
第3次旋转路线是以正方形的边长为半径，以90°圆心角的扇形，路线长为$\frac{90π×1}{180}$=$\frac{1}{2}$π；
第4次旋转点O没有移动，旋转后与最初正方形的放置相同，
因此4次旋转，顶点O经过的路线长为$\frac{1}{2}$π+$\frac{\sqrt{2}}{2}π$+$\frac{1}{2}$π=$\frac{\sqrt{2}+2}{2}$π；
∵2016÷4=504，
∴经过2016次旋转，顶点O经过的路程是4次旋转路程的504倍，即504×（$\frac{\sqrt{2}+2}{2}$π）=（252$\sqrt{2}$+504）π．
故答案为：（252$\sqrt{2}$+504）π．

点评 本题主要考查了旋转变换的性质、正方形的性质以及弧长的计算，读懂题意，并根据题意作出图形更形象直观，且有利于旋转变换规律的发现．