题目内容
10.已知a、b满足$\sqrt{4a-b+1}$+$\sqrt{\frac{1}{3}b-4a-3}$=0,求2a($\sqrt{\frac{b}{a}}$÷$\sqrt{\frac{1}{-b}}$)分析 根据非负数性质可得关于a、b的方程组,求得a、b的值代入计算即可.
解答 解:根据题意,得:$\left\{\begin{array}{l}{4a-b+1=0}\\{\frac{1}{3}b-4a-3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-3}\end{array}\right.$,
故2a($\sqrt{\frac{b}{a}}$÷$\sqrt{\frac{1}{-b}}$)
=2×(-1)×($\sqrt{\frac{-3}{-1}}$÷$\sqrt{\frac{1}{3}}$)
=-2×($\sqrt{3}$×$\sqrt{3}$)
=-2×3
=-6.
点评 本题主要考查二次根式的求值及非负数的性质,根据非负数性质列出方程组是解题的前提,代入求值是关键.

练习册系列答案
相关题目
1.在△ABC中,∠C=90°,AB=5,BC=3,则sinB=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
 如图,与∠CAB成内错角的是∠HCA,∠ABI.
如图,与∠CAB成内错角的是∠HCA,∠ABI.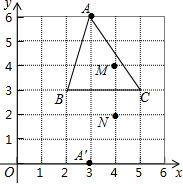 如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).
如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).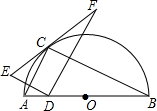 如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:
如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论: