题目内容
10.解方程组:(1)$\left\{\begin{array}{l}{\frac{x}{4}+\frac{y}{3}=7}\\{\frac{2}{3}x+\frac{1}{2}y=14}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{2x-1}{5}+\frac{3y-2}{4}=2}\\{\frac{3x+1}{3}-\frac{3y+2}{4}=0}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{3x+4y=84①}\\{4x+3y=84②}\end{array}\right.$,
①+②得:7(x+y)=168,即x+y=24③,
③×4-①得:x=12,
把x=12代入③得:y=12,
则方程组的解为$\left\{\begin{array}{l}{x=12}\\{y=12}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{8x+15y=54①}\\{12x-9y=2②}\end{array}\right.$,
①×9+②×15得:252x=516,即x=$\frac{129}{63}$,
①×3-②×2得:63y=158,即y=$\frac{158}{63}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{129}{63}}\\{y=\frac{158}{63}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
18.班长在用计算器计算全班同学期中考试数学成绩,如果他不小心遗漏了一个最低的分数,那么他计算出的结果跟实际结果相比较是( )
| A. | 偏大 | B. | 偏小 | C. | 不变 | D. | 无法确定大小 |
 .
.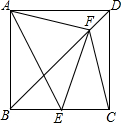 如图,正方形ABCD的边长为a,E是BC上的一点,且AE=8,F是BD上一动点.
如图,正方形ABCD的边长为a,E是BC上的一点,且AE=8,F是BD上一动点.