题目内容
1.已知|x-3y|+$\sqrt{9-{x}^{2}}$=0,求yx的平方根.分析 根据非负数的性质列方程求出x、y的值,然后代入代数式求解,再根据平方根的定义解答.
解答 解:由题意得,$\left\{\begin{array}{l}{x-3y=0}\\{9-{x}^{2}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-1}\end{array}\right.$,
所以,yx=13=1,
或yx=(-1)-3=-1,
∵1的平方根是±1,
-1没有平方根,
∴yx的平方根是±1.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
12.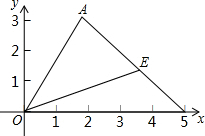 如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )
如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )
 如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )
如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )| A. | 5 | B. | 7.5 | C. | 10 | D. | 15 |
9.关于x的方程$\frac{2x-a}{x-1}$=1的解是正数,则a的取值范围是( )
| A. | a>-1 | B. | a>1且a≠2 | C. | a<-1 | D. | a<-1且a≠-2 |
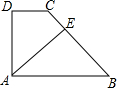 已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E.求证:CD=CE.
已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E.求证:CD=CE.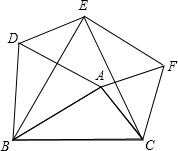 (1)感知:如图,分别以△ABC的三边为边长,在BC边的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE、EF,试猜想四边形ADEF的形状,并证明你的猜想.
(1)感知:如图,分别以△ABC的三边为边长,在BC边的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE、EF,试猜想四边形ADEF的形状,并证明你的猜想.