题目内容
17.已知在Rt△ABC中,∠C=90°,a=$3\sqrt{2}$,c=$6\sqrt{2}$,解这个直角三角形.分析 首先根据勾股定理推出b的长度,然后根据a和c的关系即可推出∠A的度数,既而求出∠B的度数.
解答 解:∵∠C=90°,a=$3\sqrt{2}$,c=$6\sqrt{2}$,
由勾股定理得:b=$\sqrt{{c}^{2}-{a}^{2}}$=3$\sqrt{6}$,
∴sinA=$\frac{a}{c}$=$\frac{\sqrt{3}}{3}$,
∴∠A≈37°,
∴∠B=90°-∠A=53°.
点评 本题考查了解直角三角形,勾股定理的应用,能通过解直角三角形求出sinA是解此题的关键,难度适中.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
8.如图图形是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.若扇形的圆心角为60°,半径为6,则该扇形的弧长为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
2.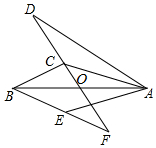 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
9.若A是五次多项式,B是三次多项式,则A+B一定是( )
| A. | 五次多项式 | B. | 八次多项式 | C. | 三次多项式 | D. | 次数不能确定 |
4.下列根式中,是最简二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{12}$ | C. | $\sqrt{5}$ | D. | $\frac{1}{\sqrt{3}}$ |
 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( ) B.
B.  C.
C.  D.
D. 