题目内容
10.已知关于x的一元二次方程$\frac{1}{2}$mx2+mx+m-1=0.(1)若该方程有两个相等的实数根,求m的值;
(2)若该方程的一个根为-2,求m的值及该方程的另一个根.
分析 (1)根据一元二次方程的定义及判别式的意义得到m≠0且△=m2-4×$\frac{1}{2}$m(m-1)=0,然后解方程即可得到满足条件的m的值;
(2)把x=-2代入原方程得出2m-2m+m-1=0,求出m的值,由根与系数的关系来求方程的另一根.
解答 解:(1)根据题意得,m≠0且△=m2-4×$\frac{1}{2}$m(m-1)=0,
解得m1=0(舍去),m2=2,
则m的值为2;
(2)解:把x=-2代入原方程得出2m-2m+m-1=0,
则m=1,
∴方程为x2+2x=0
又∵x1+x2=-2,
∴x2=0,
∴m的值为1,该方程的另一个根为0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系,以及根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
2.某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
| A. | x (x-10)=200 | B. | 2x+2 (x-10)=200 | C. | x(x+10)=200 | D. | 2x+2(x+10)=200 |
18. 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )| A. | 40cm | B. | 6cm | C. | 8cm | D. | 10cm |
5.若扇形的圆心角为60°,半径为6,则该扇形的弧长为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
2.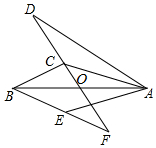 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
 如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )
如图,△ABE和△ADC分别沿着边AB、AC翻折180°形成的,若∠BCA:∠ABC:∠BAC=28:5:3,BE与DC交于点F,则∠EFC的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
 如图,四边形ABCD是⊙O内接四边形,$\widehat{BD}$=$\widehat{AD}$,求证:CD平分∠ACE.
如图,四边形ABCD是⊙O内接四边形,$\widehat{BD}$=$\widehat{AD}$,求证:CD平分∠ACE.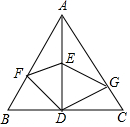 如图,在边长为8的等边三角形ABC中,点E是中线AD的中点,点F在AB边上,点G在AC边上,则由线段DG、GE、EF、FD围成的图形周长最小值等于12.
如图,在边长为8的等边三角形ABC中,点E是中线AD的中点,点F在AB边上,点G在AC边上,则由线段DG、GE、EF、FD围成的图形周长最小值等于12.