Question

6．如图，△ABC，△DCE都为等腰直角三角形，B、C、E三点在同一直线上，BF∥DE，DF交BE于G，且G为BE的中点：
（1）若AB=2，CE=$\sqrt{2}$，求△ACD的面积；
（2）求证：DG=FG；
（3）探索AG与FD的位置关系，并说明理由．

Answer 1

分析 （1）由等腰直角三角形的性质得出∠ABC=∠ACB=∠E=45°，AC=AB=2，CE=$\sqrt{2}$CD=$\sqrt{2}$，得出CD=1，证出∠ACD=90°，即可得出△ACD的面积；
（2）由ASA证明△DEG≌△FBG，即可得出DG=FG；
（3）连接AF，由全等三角形的性质得出BF=DE=CD，证出∠ABF=∠ACD，由SAS证明△ACD≌△ABF，得出AF=AD，由等腰三角形的三线合一性质即可得出结论．

解答 （1）解：∵△ABC，△DCE为等腰直角三角形，
∴∠ABC=∠ACB=∠E=45°，AC=AB=2，CD=DE，CE=$\sqrt{2}$CD=$\sqrt{2}$，
∴CD=1，
∵∠ACD=180°-45°-45°=90°，
∴△ACD的面积=$\frac{1}{2}$AC×CD=$\frac{1}{2}$×2×1=1；
（2）证明：∵BF∥DE，
∴∠GBF=∠E=45°，
∵G为BE的中点，
∴BG=EG，
在△DEG和△FBG中，
$\left\{\begin{array}{l}{∠E=∠GBF}&{\;}\\{BG=EG}&{\;}\\{∠BGF=∠CGD}&{\;}\end{array}\right.$，
∴△DEG≌△FBG（ASA），
∴DG=FG；
（3）解：AG⊥FD，理由如下：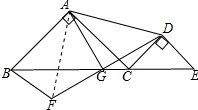
连接AF，如图所示：
由（2）得：△DEG≌△FBG，
∴BF=DE=CD，
∵∠ABF=∠ABC+∠GBF=90°，
∴∠ABF=∠ACD，
在△ACD和△ABF中，
$\left\{\begin{array}{l}{AC=AB}&{\;}\\{∠ACD=∠ABF}&{\;}\\{CD=BF}&{\;}\end{array}\right.$，
∴△ACD≌△ABF（SAS），
∴AF=AD，
又∵DG=FG，
∴AG⊥FD．

点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、平行线的性质；熟练掌握等腰直角三角形的性质，证明三角形全等是解决问题的关键．